22 Nov 2022

Receipts for BMS Ep 254: Kark Marx Was Kind of a Big Deal

All Posts 9 Comments

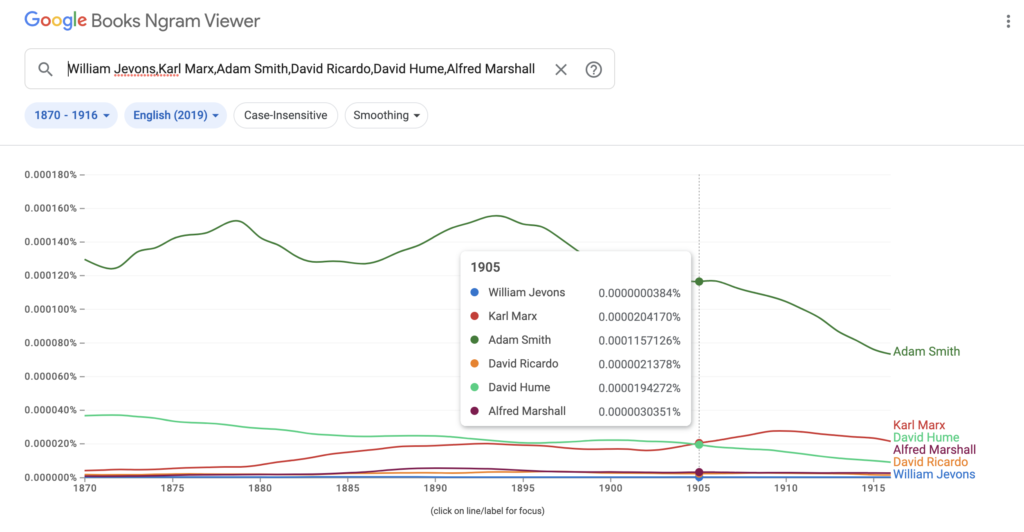
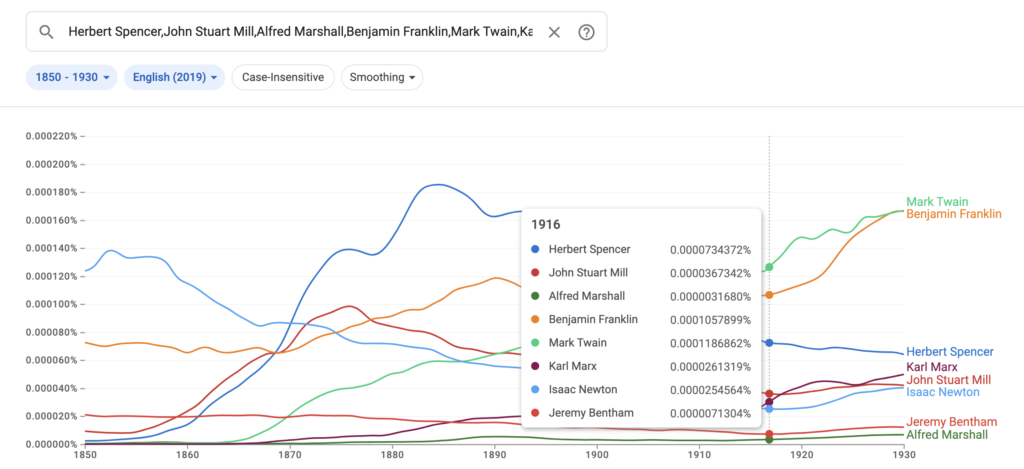
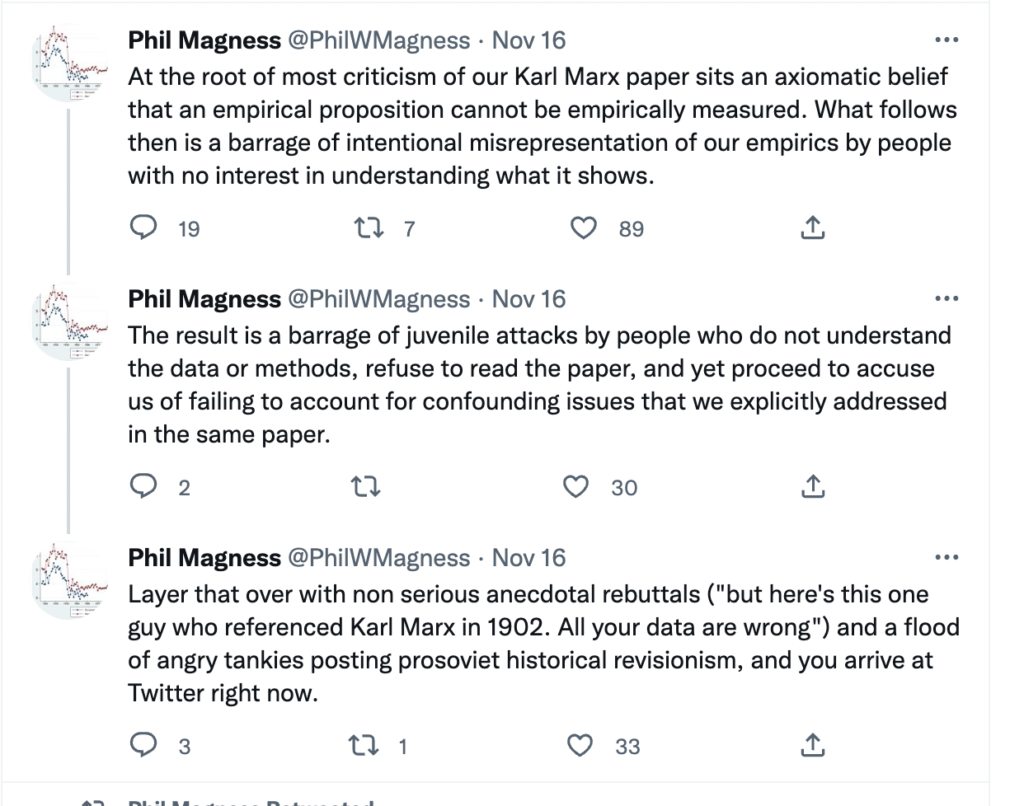
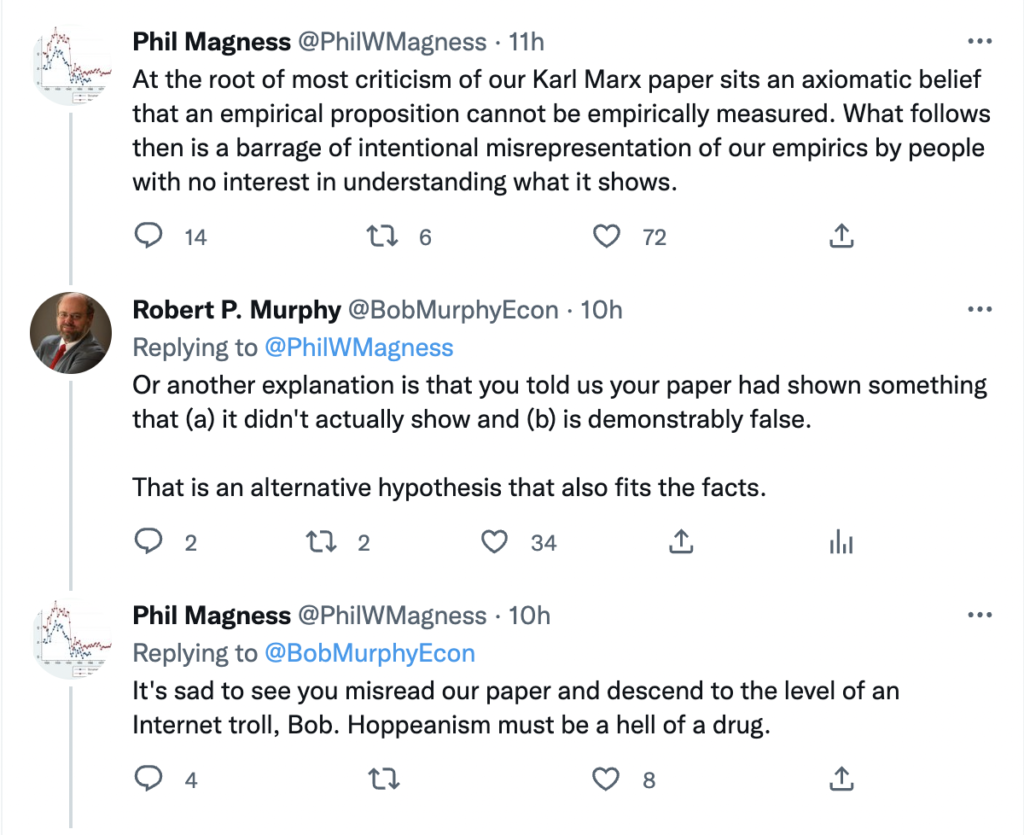
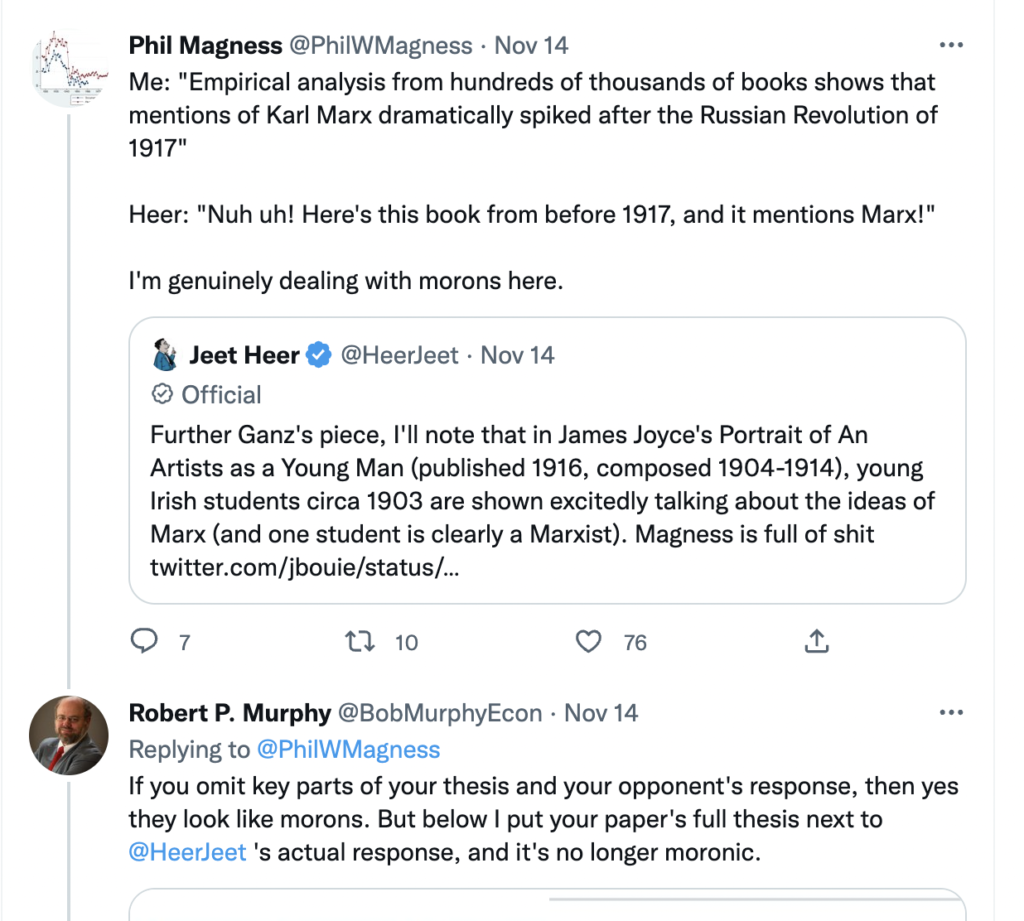
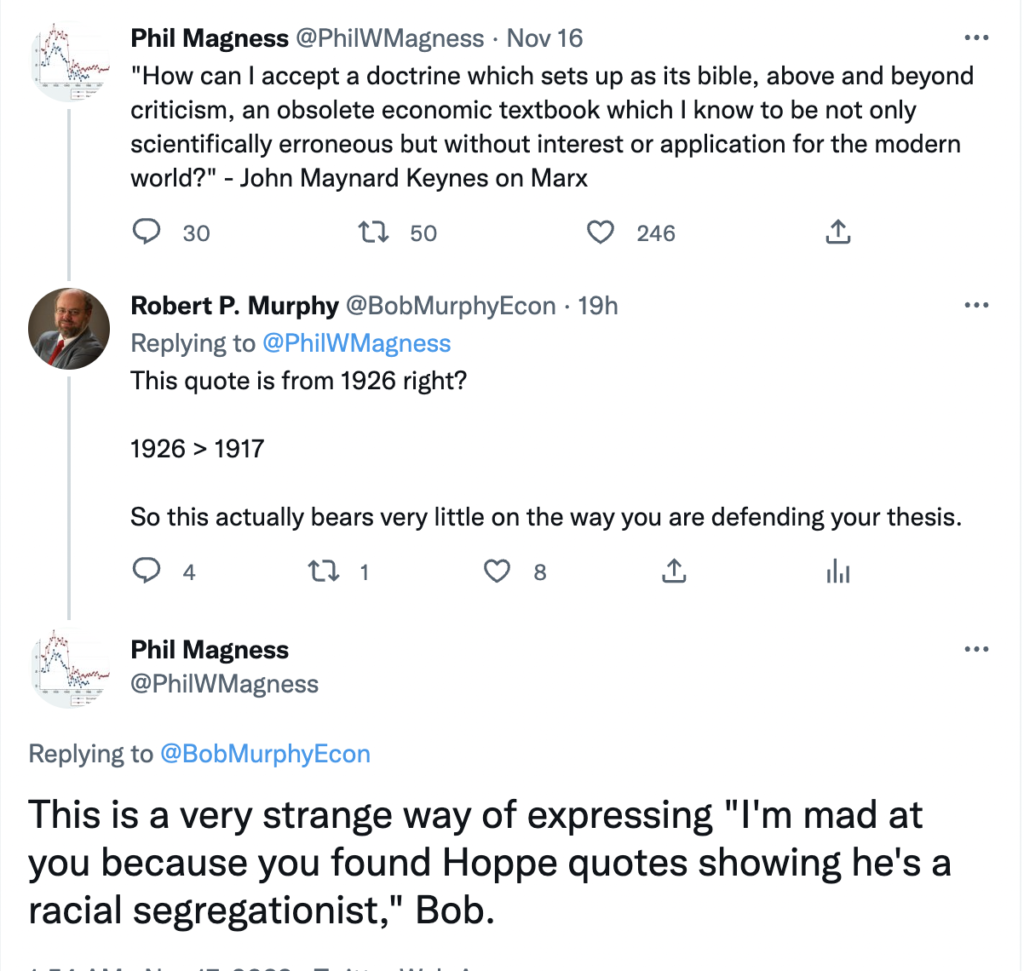
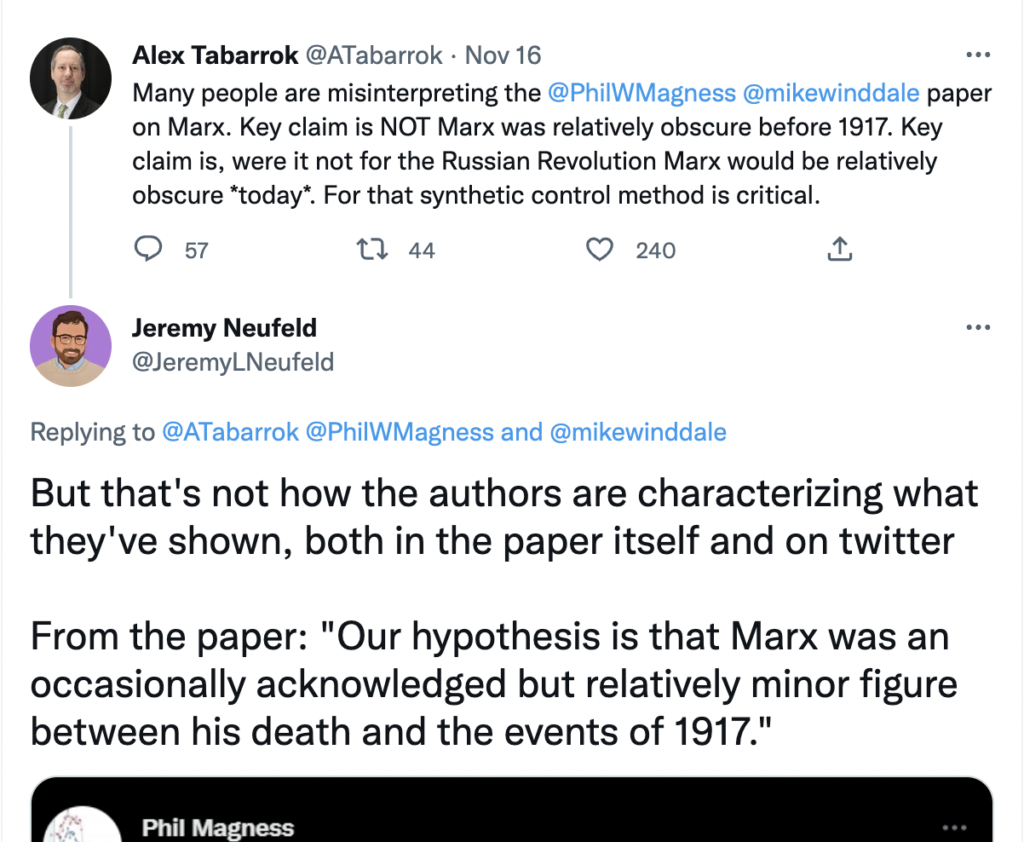
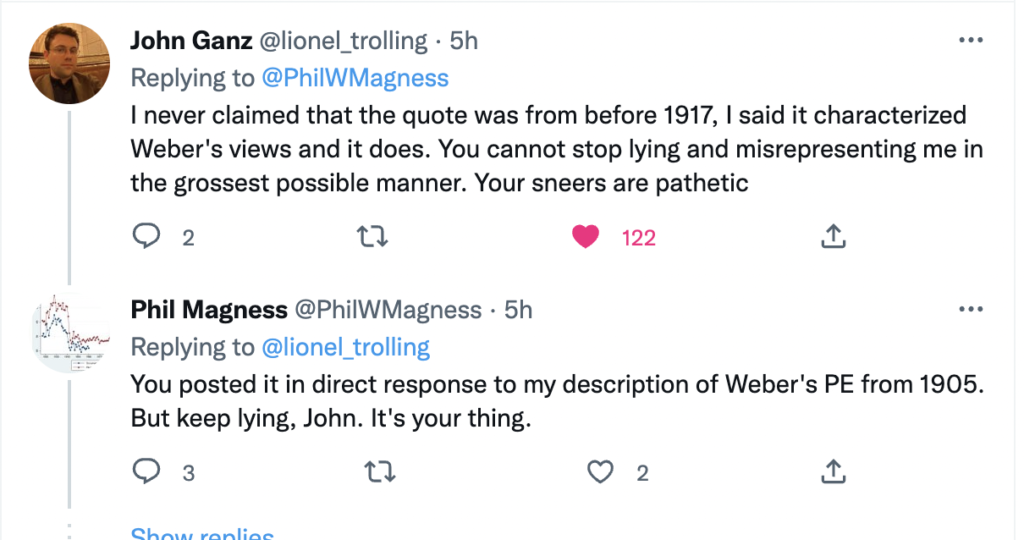
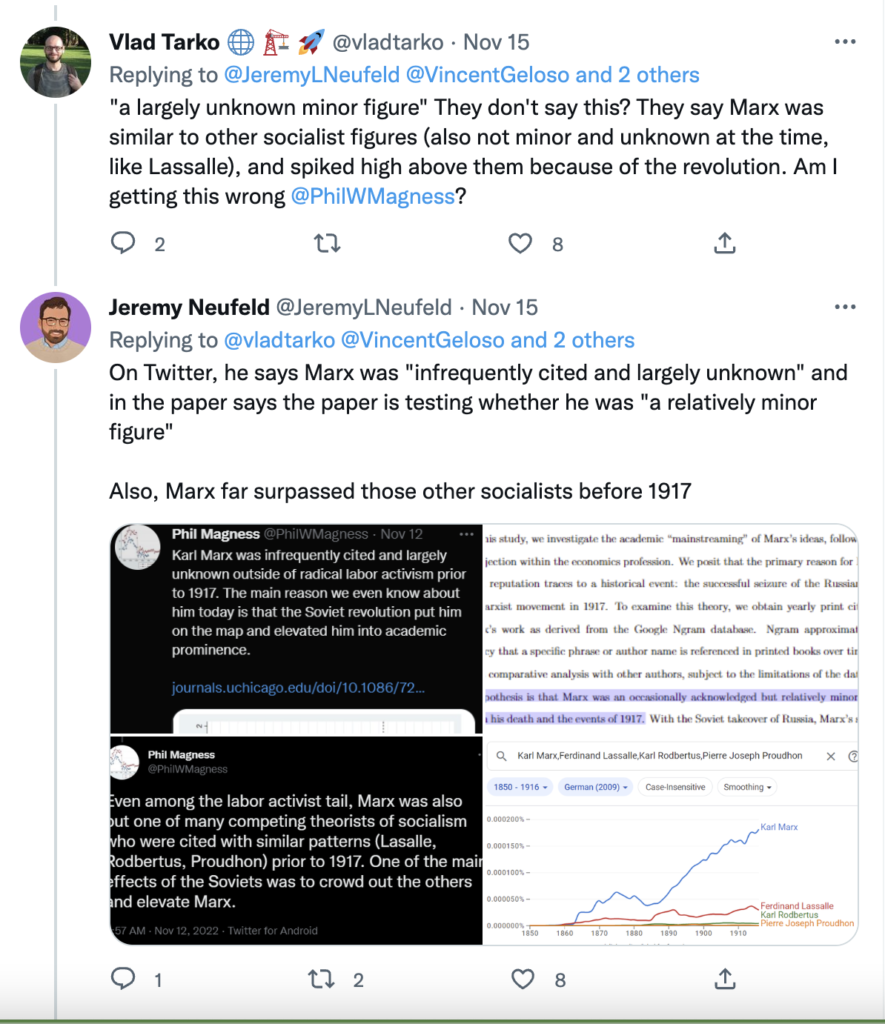
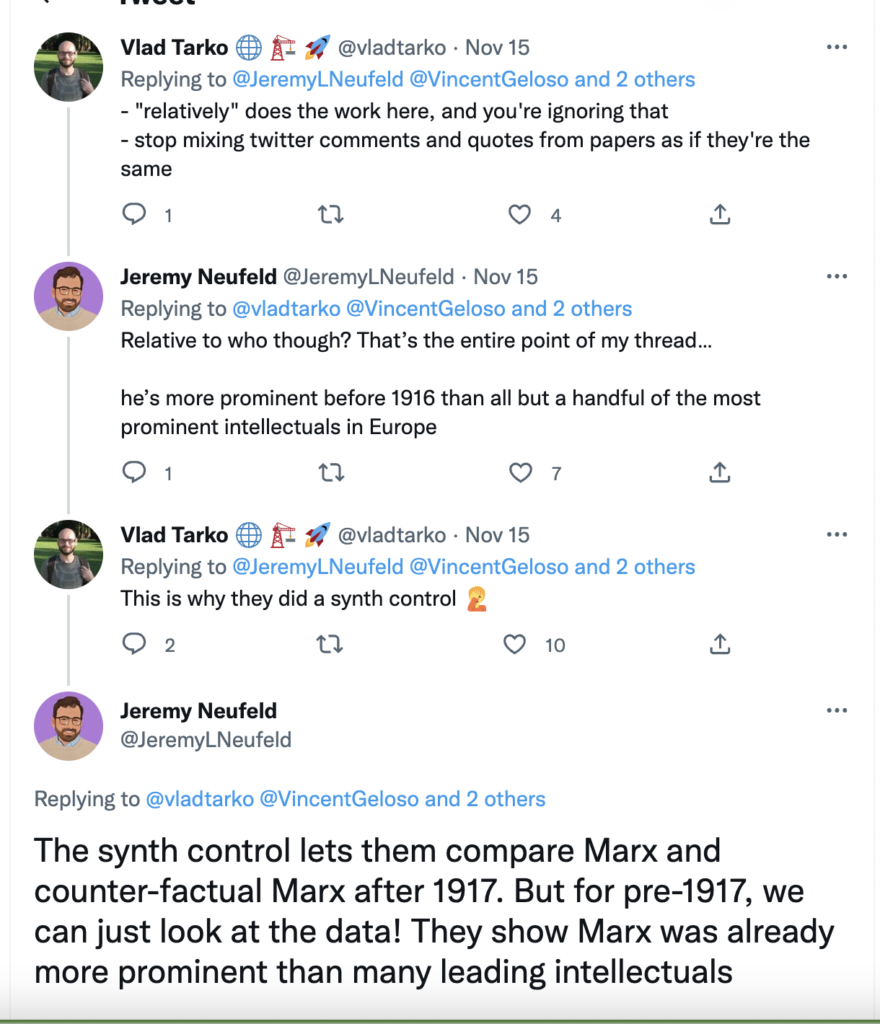
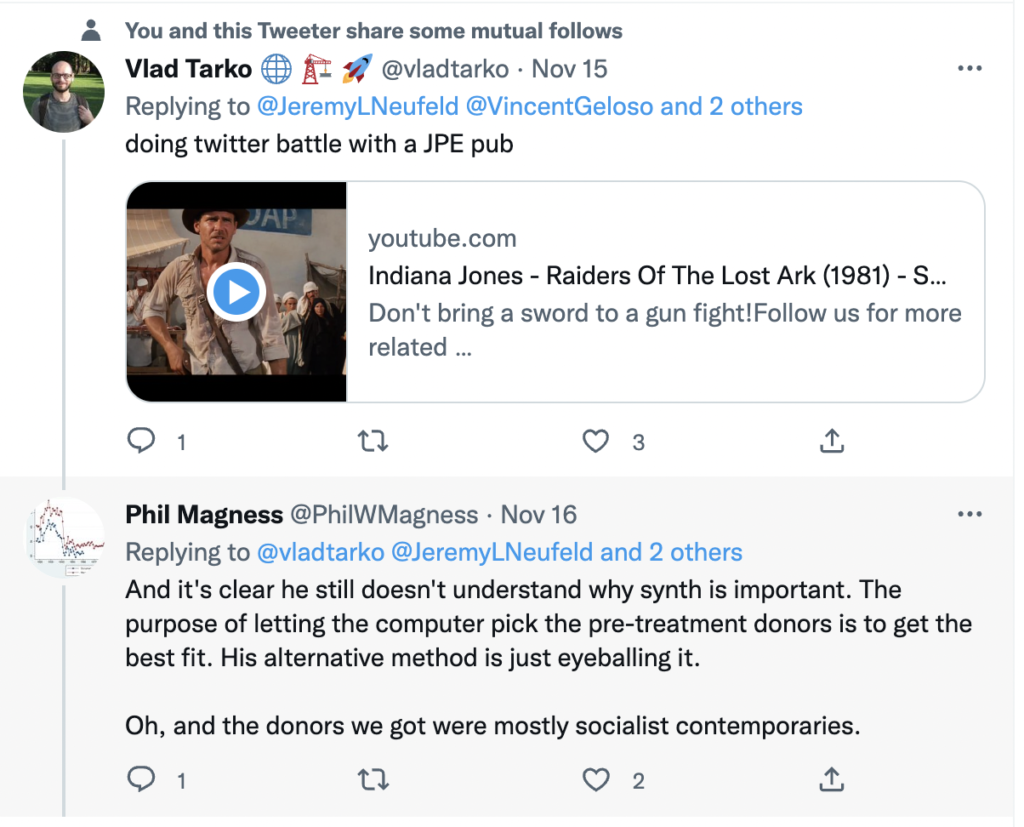
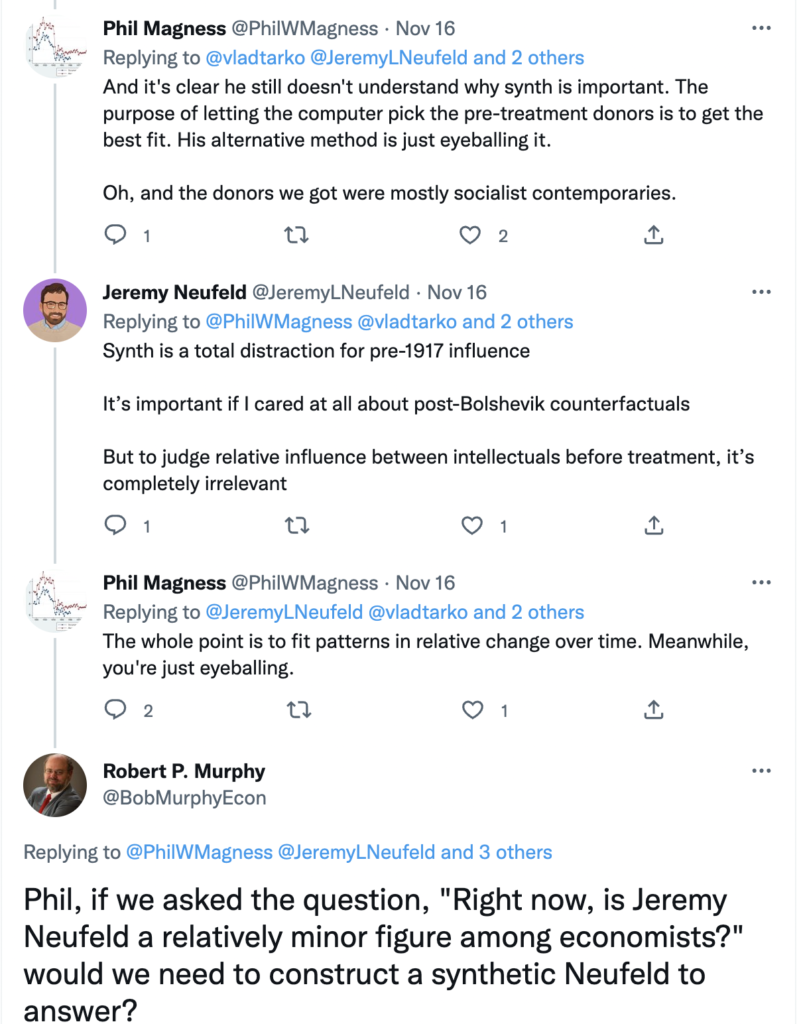
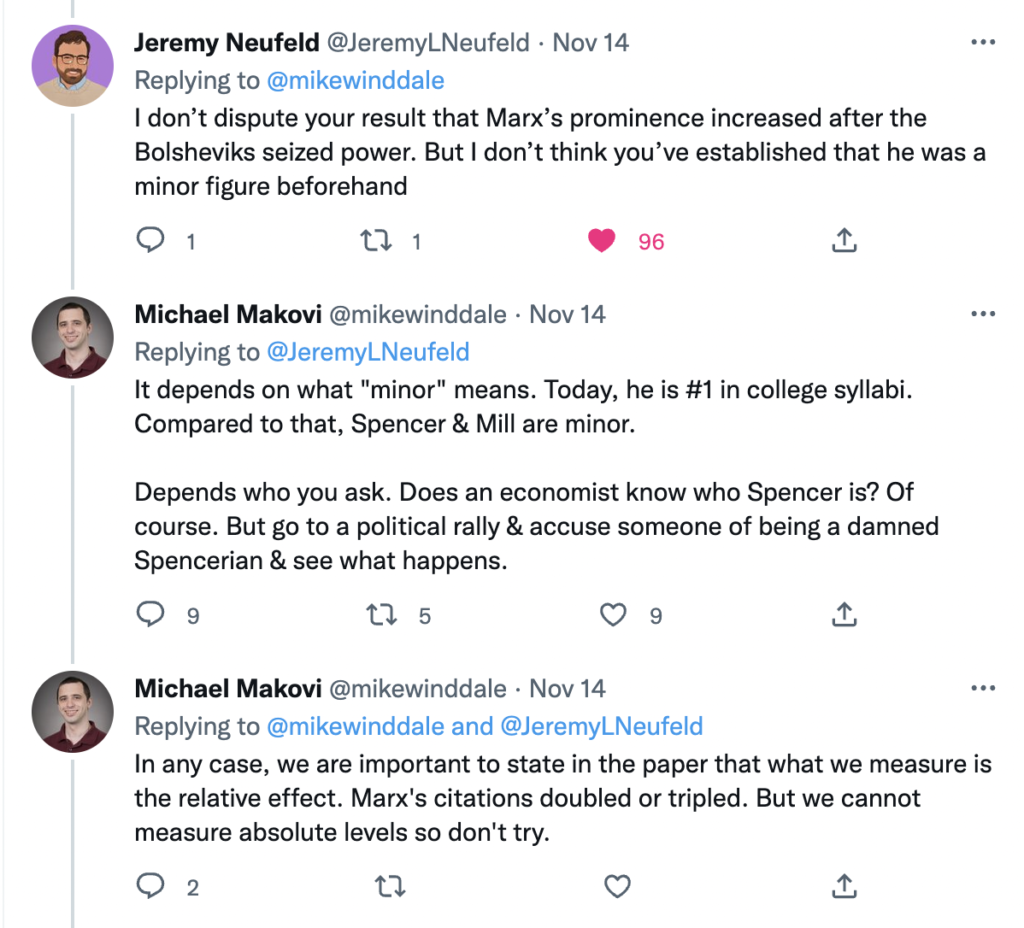
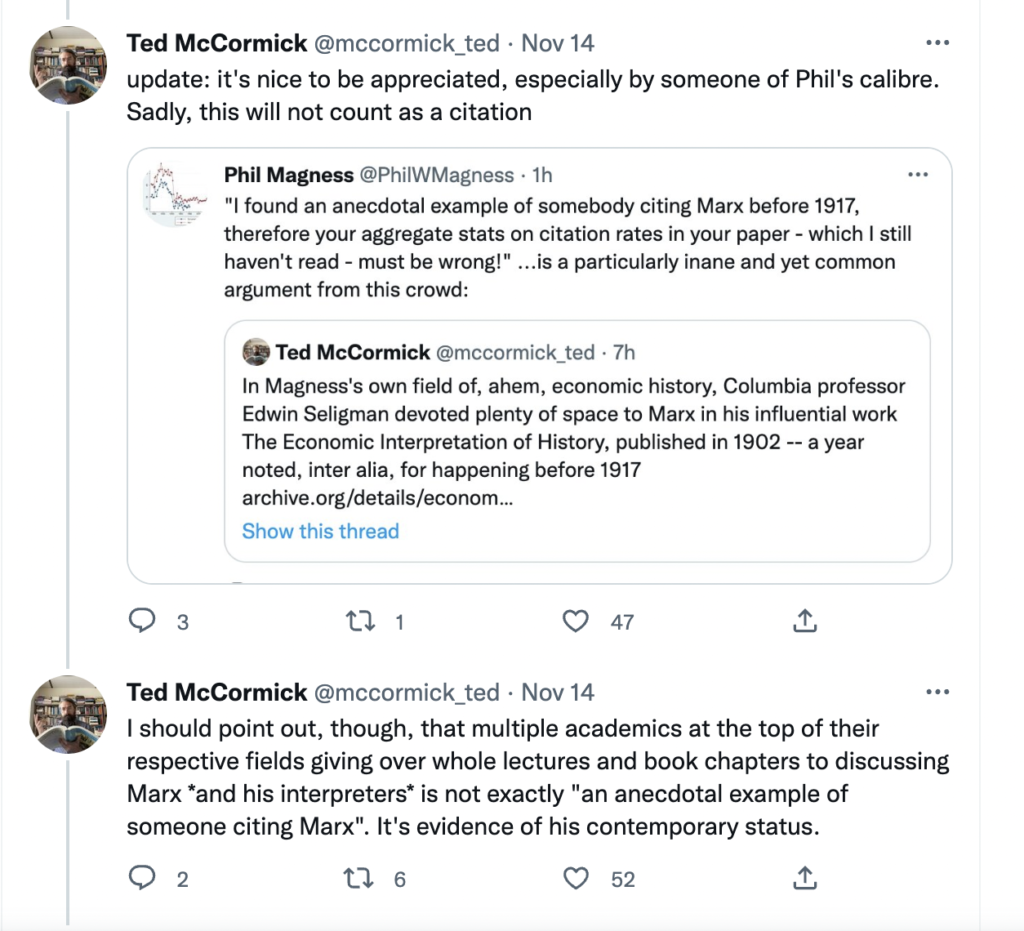
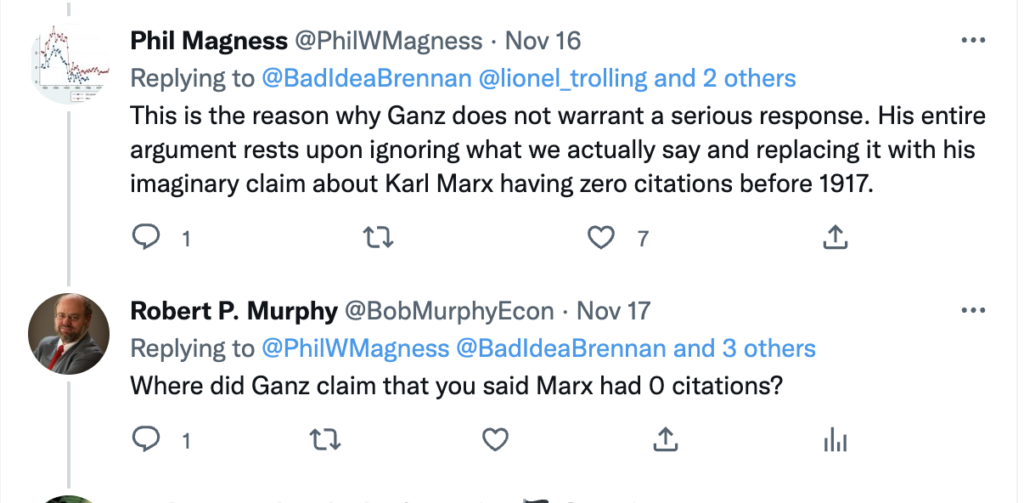
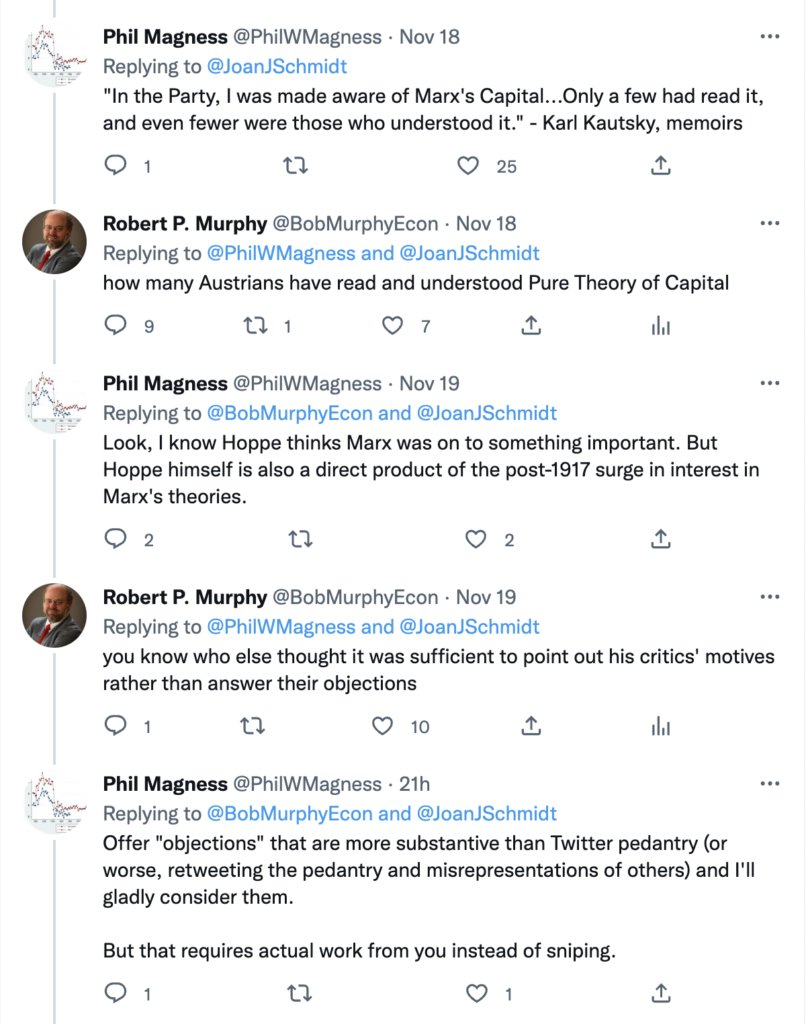
Here is the link to my podcast critique of Phil Magness’ promotion of his paper, co-authored with Michael Makovi, on Karl Marx. In this episode I allude to many things, some of which I document below, so listeners can see I’m not putting words in anyone’s keyboard.

02 Jun 2022

My Talk at Orlando

All Posts 51 Comments
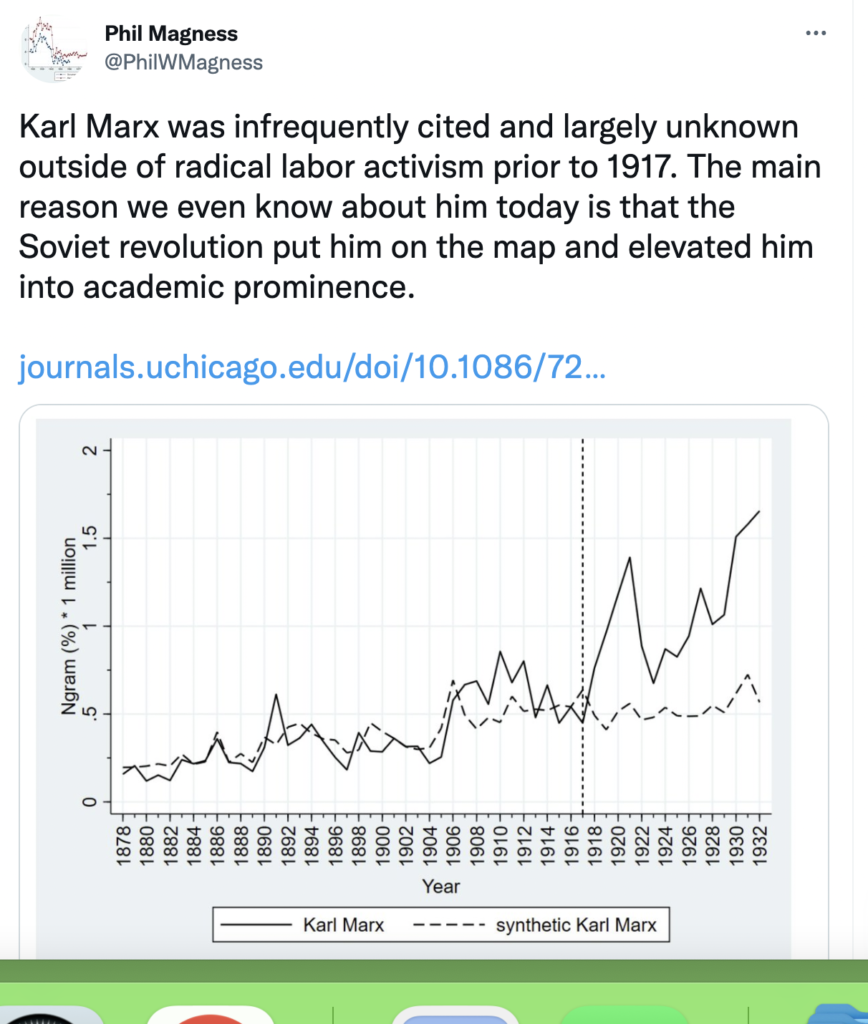
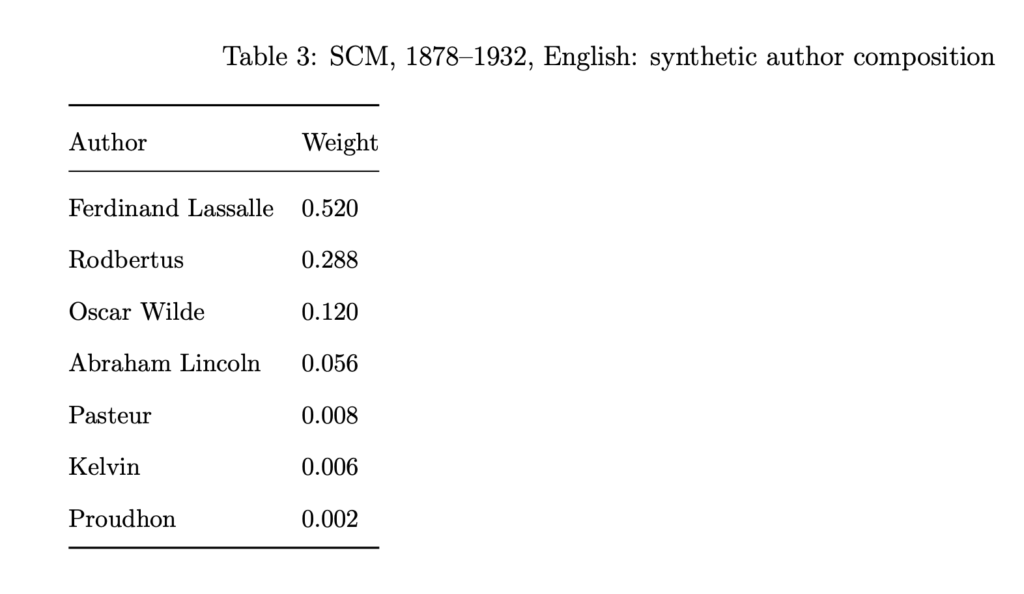
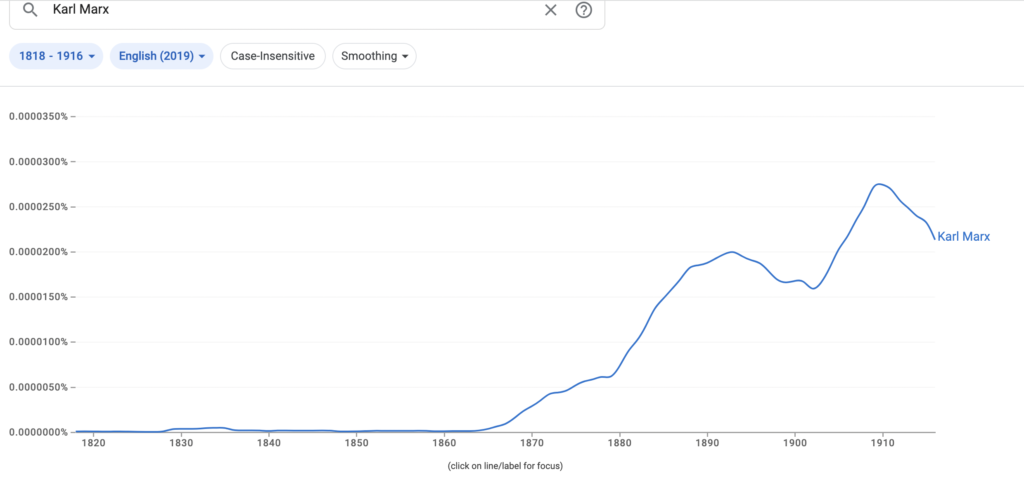
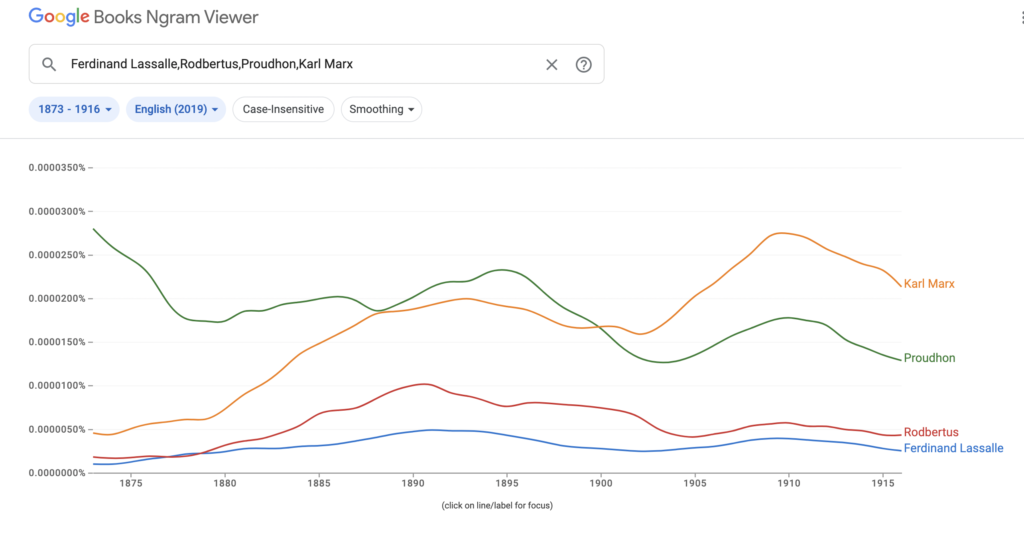
08 Apr 2022

New Episodes of BMS and LMS

All Posts 53 Comments

Bob Murphy Show ep. 235 is my Part 5 on Klaus Schwab.

Ep. 82 of the Lara-Murphy Show features a revisitation of our “How to Weather the Coming Financial Storms” presentation.

And here’s a short video I made for a college panel on Austrian economics:

21 Mar 2022

Jeff and Bob Discuss Economic Ignorance

All Posts 4 Comments
17 Mar 2022

BMS eps 232 and 233

All Posts 18 Comments

Episode 232 and 233 continue my series on Klaus Schwab and the Great Reset.

14 Mar 2022

Jeff Deist and I Talk Oil Prices

All Posts 2 Comments
09 Mar 2022

BMS ep. 231 Thad Russell Repeatedly Lied to Michael Malice

All Posts 3 Comments

Oops I missed this one.

09 Mar 2022

BMS ep. 232: Behind Klaus Schwab, Part 3

All Posts No Comments

Some juicy audio clips in the beginning of this one…