More on Flood Statistics
In my previous post, there was still some confusion in the comments. And on Twitter, I got the sense that even trained economists didn’t understand what the big deal was.
So remember, the claim is that the phrase “100-year flood event” or “500-year flood event” is very misleading. When the government data agency gives such a designation, it is referring to the probability of an annual occurrence. For example, a “100-year flood event” is defined as “a flood event that has a 1% probability of occurring in any particular year.” People erroneously think that means the same thing as, “We expect a flood like this to happen once per century,” but no, that’s not really what it means.
Let’s imagine instead that we’re talking about a “4-year flood event.” In other words, there is a 25% chance each year that we’ll see a flood of this magnitude.
Now, over a given 4-year stretch, what is the expected number of such floods? More specifically, what is the mathematical expectation of the number of floods we’ll observe?
One way to calculate this is to say each year we have an expectation of 0.25 floods, times 4 total years, means an expectation of 1.0 floods over the course of 4 years.
However, is that the same thing as saying, “We expect to see 1 flood over a 4-year stretch?”
I don’t think so. First, let me ask a different question: “Do you expect it to rain tomorrow?”
How do you answer? Surely, if the person thinks there is less than a 50% chance of rain tomorrow, then he can’t possibly answer, “Yes I expect it to rain tomorrow.” Right?
So by the same token, if you think there is less than a 50% probability that we will see 1 flood during a 4-year stretch, then it is arguably incorrect to say, “I expect to see 1 flood during a 4-year stretch.”
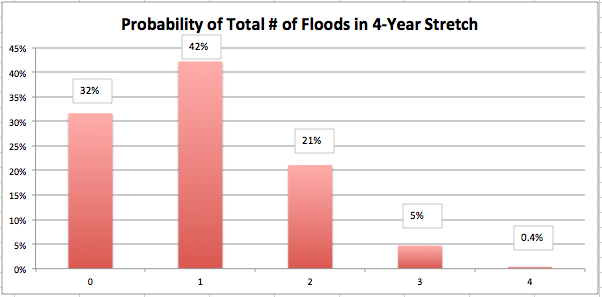
Here’s the actual breakdown of possible outcomes:
As the chart shows, there is only a 42% chance that we will observe exactly 1 flood during any 4-year interval. So if someone asks me, “Do you expect 1 flood to occur in the next 4 years,” I could plausibly answer, “No, because there is a 58% chance that something besides 1 flood will occur.”
This isn’t just a matter of semantics. It can definitely mislead people in certain settings.
For example, when people learn that their house is located in a “100-year flood zone,” they think their house is only going to get hit with a flood “once per century,” and so they might not buy flood insurance.
However, since what this actually means is that there is a 1% chance each year of such a flood, we can tell such a homeowner that over the course of his 30-year mortgage, there is a 26% chance of being hit by such a flood at least once. That sounds a lot more deserving of flood insurance than, “You’ll get hit by a flood like this once a century.”







A naive estimate might be that over a 30 year period there would be a 30% chance of a hundred year flood. 26% sounds quite reassuring.
If my calculations are right: There is a 36% chance that the 1 in 100 year event may not occur at all in a given 100 year period. and a 13% chance that it will not occur even in a 200 year period. There is also a 36% chance it will occur only once in a given 100 years.
That is quite high for 200 years – statistics has some non-intuitive outcomes. I do not doubt your calculations.
If were to toss a coin twice we have an expected outcome of 1 head, but nobody would be at all surprised if got no heads, or 2 heads. Similarly for 100 year floods, we have an expected outcome of 1 flood, but we should not be surprised if we get none, or several.
Somehow going from 50% to 1 % makes it much harder to intuitively grasp this.
Gene refers to Fivethirtyeight.com in his post. During election season they are constantly repeating that their probability % of winning means that if the calculated % is x% then the race has to be repeatedly run, under identical circumstances, for the % to be proven correct. A failure to understand this lead to the post-election hysteria on the left
“So by the same token, if you think there is less than a 50% probability that we will see 1 flood during a 4-year stretch, then it is arguably incorrect to say, “I expect to see 1 flood during a 4-year stretch.””
Yeah, maybe “arguably” incorrect. But when I say “I expect”, I’m typically using that word in the sense of mathematical expectation. I see why you think that this statement is wrong and I also see why the commenters (myself included) had no idea what you were talking about even though they understand expectation, i.e. E[X].
Incidentally, it seems perfectly reasonable to me to worry about 1,000-year floods when you buy a house. Over your lifetime, you expect to see something like 0.085 of those….. sigh…. on average you will see 0.085 of those. If your house has something like a 5-10% chance of being completely wrecked by a flood at some point (which I think a 1000-year flood would do) then insuring against this sounds pretty reasonable to me.
In fact that sounds like exactly the sort of event you should insure against. (No point in insuring against things with a 100% chance of happening, and arguably you might not want to insure against 1 in a million events, but 5% events scare me.)
“As the chart shows, there is only a 42% chance that we will observe exactly 1 flood during any 4-year interval. So if someone asks me, “Do you expect 1 flood to occur in the next 4 years,” I could plausibly answer, “No, because there is a 58% chance that something besides 1 flood will occur.””
This still strikes me as disingenuous. First of all, it seems weird to bucket “zero floods” and “three floods” together in the bucket of “amount of floods other than one.”
But secondly, as I said in the last comment, if you held a gun to my head and said “Predict how many floods will occur over the next four years,” one is still clearly, obviously, the best answer, even if it’s only 42% likely to be accurate.
Matt M wrote: “This still strikes me as disingenuous.”
I really think people are misunderstanding the point of these posts. I’m not saying that anybody who claimed, “I expect one of these floods every century” is a liar or is wrong.
Rather, I’m pointing out that the statistical meaning of “expectation” doesn’t line up perfectly with the everyday notion of “expect.”
It’s not just a brain teaser parlor trick, I think regular people draw the wrong conclusions when they hear that Houston just had a “500 year flood event.” Among other things, I think many people assume that means, “We checked the records and there hasn’t been this much flooding in Houston at least back to 1517,” which it clearly does NOT mean.
Exactly correct. “Expectation ” is a technical term, not quite aligned with the normal meaning of expect.
Imagine a storm guaranteed to hit in every year ending in 17 and in no other year. The expectation would still be one in a hundred years, and that,s what we’d all expect and count on.
I refuse to believe there are any adults of normal mental function who take the Harvey coverage to mean something like “The last time a storm like this occurred was 1517 and the next time one will occur is 2517”
Submit it for your incredulity
https://www.cbsnews.com/news/what-does-500-year-flood-really-mean/
*Submitted
Matt M what are you talking about? *I* thought the headlines originally meant, “We haven’t seen a flood this bad in 500 years.” I hope I have at least normal mental function.
To be clear, I didn’t *believe* the claim, but I thought that’s what they were trying to tell people.
Well, in lieu of calling Bob an idiot (which would make for an awkward cruise next month), I’ll retract my statement. I thought it was self-evidently obvious that the point of the claim was to say “this is the amount of water that, on average, we would expect to happen about once every 500 years” rather than “the last time we saw a flood like this was 500 years ago.” I guess I was wrong.
I think part of the issue is, I was seeing so many people linking it to climate change, where people all the time say things like, “The hottest summer on record,” “the most rainfall as far back as our records go,” etc.
And I, on the other hand, kept thinking about how a lot of coverage was simultaneously saying “this was so much worse than anyone expected” which seems contradictory.
If we knew when the last time it flooded like this was, and we knew it would flood like this every 500 years, then we absolutely should have expected this!
And certainly nobody seems to be saying, “Whew, glad we got that out of the way, no need to prepare for that again, it won’t flood this badly in Houston again until 2517!”
Can you just give me a quick refresher on the meaning of “normal” ?
Because every time I think I’ve got it, I seem to keep getting left behind.
As a professional who deals with flooding from time to time. Here is an alternate view of the probabilities..
If you have 500 locations, you would have the following flooding expectations each year:
1 – 500 year flood
5 – 100 year floods
10 – 50 year floods
20 – 25 year floods
If your a national broadcast firm you can find a 100 year storm somewhere in the US each week, and a 500 year storm every year.
Hurricanes come in batches and they sweep a broad area so there’s a strong correlation in both space and time. Check the years here:
https://en.wikipedia.org/wiki/List_of_Category_5_Atlantic_hurricanes
There was a whole bunch in the 1930’s, then none at all in the 1940’s. Similarly, there were a number in 2005 and 2007 and then all quiet until 2016.
Data again. You sneaky bastard!
So I’m told, “Data is the new bacon”.
I happen to find the good old fashioned bacon is also quite satisfying.
Allow me to once more draw attention to the work of Lorenz and the question of whether a stochastic approach is valid for analysis of a chaotic system (or course it isn’t strictly valid, but the real question is how bad is the estimate and how to we make allowance for that).
And you haven’t even had to get into standard deviations yet.
This seems to put a whole lot of emphasis on the question of whether “expected value” and “whether the probability associated with a given outcome is greater than 50%” are the same thing, which they’re obviously not – and it obscurest that that’s what you’re doing by switching between multiple outcomes (number of hurricanes) and dichotomous outcomes (rain/doesn’t rain).
That doesn’t seem right. Expected value is the one to go with. We do expect one of these every hundred years, but that expectation doesn’t mean one storm has greater than fifty percent probability.
I hope you use expected value and not “is the percentage greater than 50%” when you make investment decisions.
Daniel wrote:
We do expect one of these every hundred years…
Well yes, if you just assert, and dismiss the obvious sense in which your claim is wrong, then you win the argument. I don’t deny that.
I hope you use expected value and not “is the percentage greater than 50%” when you make investment decisions.
I guess it would depend on whether I invested based on headlines that said, “Once In a Lifetime Opportunity.”
And also, to continue with your analogy, the whole point of 538’s article was that people were making bad investment choices (i.e. whether to buy flood insurance or not) because of the potentially confusing nomenclature.
I guess the 538 people should’ve checked with you first, so you could clarify, “We do expect one of these every 100 years,” when the whole point of their article was to say a lot of people don’t know what you mean when you say that.
Daniel wrote:
This seems to put a whole lot of emphasis on the question of whether “expected value” and “whether the probability associated with a given outcome is greater than 50%” are the same thing, which they’re obviously not – and it obscurest that that’s what you’re doing by switching between multiple outcomes (number of hurricanes) and dichotomous outcomes (rain/doesn’t rain).
No Daniel, I don’t think this is right.
If I ask people, “Do you expect to roll a 3.5 on your next die roll?” are you telling me it’s ludicrous for someone to answer, “No” ?