Do “Productivity” and Lagging Wage Growth Disprove Marginal Productivity Theory?
In response to my book review of Piketty, where I claimed in my cutesy “Jetsons” example that a slow-down in capital accumulation would reduce the growth in workers’ real incomes, people have been throwing BLS charts in my face. To take an example from today, on Twitter:
@libertarianJ @PorphyConob @BobMurphyEcon "more physically productive per hour, and hence will be paid more." No
http://t.co/2mySdSfRns
— Professor Zaius (@ProfessorZaius) June 3, 2014
This is the paper to which he links. From that paper, here’s the money chart that supposedly blows up my claim that workers get paid more as capital accumulates:
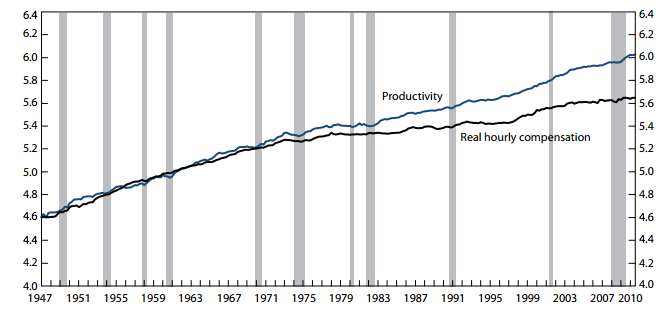
Yikes! Everyone see the outrage? The productivity of labor has been rising nicely for decades, and yet real labor compensation hasn’t kept up. Therefore, according to my critics, I’ve got my head buried in my Econ 101 textbook and need to look out the window at the real world. Workers apparently don’t get paid more, even as accumulating capital goods make their labor hours more physically productive.
I will do a more comprehensive response elsewhere, but here I just want to post the results of a simple Excel demonstration. I used a version of the Solow growth model, but instead of the usual “Cobb-Douglas” functional form, I picked one that allows for the factors of production (i.e. capital and labor) to earn different shares of total output, depending on which one grows faster.
I’m not going to dwell too much here on the meaning of it all. Just note in the screenshots below that capital and labor both earn their marginal products; there is no “exploitation” going on here. And yet “productivity”–which the BLS defines as total output divided by unit of labor input–grows much faster than the real wage rate. So once you wrap your head around my example below, look again at the chart above and see if it changes your interpretation of what it means for marginal productivity theory, and my claims about Piketty.
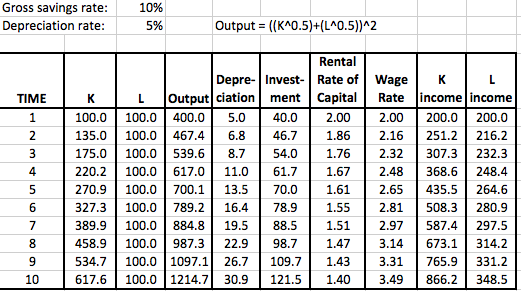
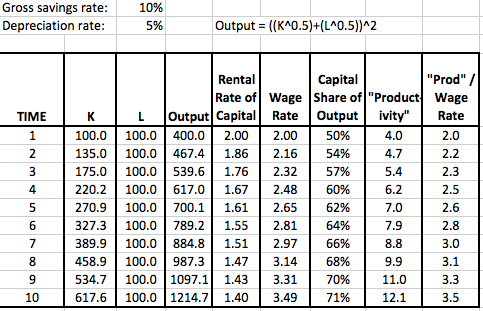
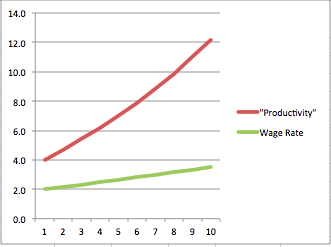







Nice!
Are you saying that this is the explanation for why wages have not matched productivity growth since 1970, or just that it is possible to build a model where wages don’t keep up with productivity growth even though workers are still being paid their full marginal product ?
Transformer, strictly speaking I’ve just shown that the data are consistent with every factor being paid its marginal product. But if you click the Twitter link, you’ll see his point was merely that capital’s share has risen. Right, which doesn’t at all contradict my claim about Piketty hurting the absolute incomes of workers (relative to baseline).
But, I also do think that factors generally get paid their marginal product in a market economy, or at least, that there is a tendency for them to be paid it. But I’ll discuss this more in my “big picture” Mises CA post. This post here is more of a technical appendix to illustrate my sweeping generalities.
Aren’t they arguing that as K increases, L would decrease? In your scenario, K keeps rising but L stays locked at 100.
Isn’t that their real point? As capitalists accumulate more and more capital (and invent robots), the demand for labor diminishes, and therefore the price that labor is able to command for its services falls as well?
(also thanks for posting the model, it really helps the layman like me better understand the concepts)
To disprove the claim that wages increase when productivity increases we’re shown a graph where both wages and productivity are increasing. I don’t understand.
Unrelated, but they start diverging when we left the gold standard. Coincidence?
To disprove the claim that wages increase when productivity increases we’re shown a graph where both wages and productivity are increasing. I don’t understand.
I said the same thing. If you click the Twitter link you can see the guy defend himself.
I had this problem also. No matter how hard I squint at it, that line still has positive slope. I’m not sure Professor Monkey-For-a-Head has picked data that supports his conclusion.
All that the graph proves is that we should be back on the “Gold Standard”.
Of COURSE it’s not a coincidence. The Cantillion Effect of inflation is the root cause of the divergence.
See also this 2008 paper by Martin Feldstein.
http://www.nber.org/papers/w13953
Ed Lazear at Stanford and James Sherk at Heritage (among others) have also done important work showing that the alleged “decoupling” of worker pay from worker productivity is a myth.
Am I slow tonight or did you just say “the absolute wages of the workers will rise” as well as “will be paid more” and some Professor sent back a chart showing the absolute wages of the workers rising, and hence getting paid more… along with just the comment “No” ?
Are there multiple possible meanings to “will be paid more” ?
I searched “Professor Zaius” thinking this was possibly remotely serious, only to find it is out of a movie. This is the level of current economic discussion.
And there it is, plainly obvious that when the “total output” goes up, some proportion will go to employees, and some proportion will go to entrepreneurs. Amazing!
We better get cracking if we hope to keep pace with the apes.
OK, I have no intent ot be trollish but, if you model OUTPUT = (K^.5+L^.5)^2 are you not in effect saying that yeah, it’s OK to assume you can aggregate capital (despite the Cambridge capital controversy) at least as far as trying to understand broad tendancies of capital accumulation, labor share of output and real wage changes go?
Heh glad you’re keeping me honest Captain. I would answer you like this: If someone says, “Free trade doesn’t work if a country is better at producing all goods,” then the quickest way to blow that up is to do a standard two-good example. But then if someone wrote a 700 page book that crucially depends for its results on the assumption that there are only two goods being produced, I would go nuts and say that’s crazy.
I think economist George Reisman may be correct that the MVP is false. He offers the “Productivity Theory of Wages” instead to explain real wages. See pp. 666ff in his book Capitalism (free online), where he criticizes Rothbard’s explication. I think it is essentially a fine-tuning argument, as he does not reject marginalism overall. I hope someone will provide some feedback on Reisman.
I do not know if it is true that the rich have gotten richer but, if true, what that would mean to me is that the rich now enjoy increased consumption of luxury goods, not that they are getting more than their fair share of Cap’n Crunch and Disney cruises. However, Joseph Stiglitz argues that the rich save too much/spend too little of their wealth, which creates an imbalance in the economy. If this is true, and productivity has also allegedly increased, who is consuming all these goods/services?
Hey everyone,
It’s true that I’m using the dubious Solow model of “capital is a number K” here, but I think it’s worth it to walk through some other issues. Notice how wage rate goes up with accumulating K, rental price of capital goods goes down, and yet capital-owners get higher % of total income.
Bob,
Is there a problem on the site?
I tried to post a comment as Transformer but it never appeared. I tried posting with a different user/ email address and it said “duplicate comment”
Not sure why that happened, but I think everything works now?
I still can’t post as transformer
Here is what i was trying to post
“I finally cracked and bought a copy of Piketty.
I went straight to the section where he outlines the second of his 2 laws. He explains it very clearly in my view.
The law revolves around the fact that income grows as rate g, while capital grows at rate s (net savings). This means that in the long term the capital/output ratio tends towards s/g.
All very simple and makes sense on it own terms.
What I don’t get is this (and hopeful it relates to Bob’s post):
Why in Piketty’s model does a change in s not also drive a change in g? An increase in s increases the total quantity of capital, and the income of capital-owners (who earn r*k), but it seems that no matter how much capital you get in Piketty’s model income just keeps plodding along at its existing rate of increase. This means that capitalists get a bigger share of the pie if s > g, since their income is increasing at rate s (if r stays the same) , while everyone else’s just increases at g.
Does he ever explain why g and s can be treated as totally separate variables? Logically you would expect that as the amount of capital increases it would drive higher real output and not just an increase in the capital/output ratio like it does in his model.”
What exactly are “net savings”?
Savings left after you have taken out spending for depreciation on existing capital
I’ll take a whack at this, Transformer AKA test.
My discalimer is I haven’t cracked “La Capital” and most of what I say is just coming from a review of Piketty by the (infamous ) Solow here: http://www.newrepublic.com/article/117429/capital-twenty-first-century-thomas-piketty-reviewed and Bob’s example above. If you assume an unchanging rate of saving s and some kind of “Solow like” growth model then there is a unique stable, self-reproducing s/g that the economy will tend toward regardless of its starting s/g or capital income ratio. According to Solow, Piketty assumes that the economy reaches this stable s/g and then asserts that if r>g capital owners income and wealth increases a lot faster then wage earners simply because wage earners real income grows like g and (evil, greedy, – excluding Soros) capital owners incomes and wealth grow like r. I think Bob want’s us to see that assuming a relativly constant r as Piketty does is a pretty weak assumption. I’ll also point to Steve Landsberg talking about work by others showing that Pikettys assumption of a constant rate nof NET saving is weak as well. Read here:http://www.thebigquestions.com/2014/05/30/on-piketty-and-capital/
Thanks Capt,
I agree that if we were talking about gross savings then you would hit a stable level where all savings go on depreciation and you get no more capital growth , and income growth only from technological improvements (and maybe labor-force growth.)
But Piketty explicitly talks about net savings which means that capital will keep growing for ever. But no matter how big it grows it has no effect on total income – which just keeps growing (or not) at it own independent rate.
His second law states that eventually a “stable” situation would be reached (where capital/output ratio = s/g). But even here capital just keeps on growing at the rate of net savings.
(I’m going to try that Solow link now to see what light that sheds on this issue).
The best I can come up with is that Piketty may think there is a relationship between s and g for a given economy so that a given s will generate a certain level of g – but I can’t find anything in the books that states that directly.
Not sure this will help but FWIW: If you use a Cobb-Douglas production function like:
Y=K^a*L^b with a+b<1 then if net savings rate s is assumed constant then g is going to reach a stable value over time. The exact value it reaches will depend, among other things, on s, with bigger s leading to bigger steady state g but regardless of the exact value of s, s/g will always stabilize. This will be true for pretty much any production function with diminishing returns to scale. If you think you know what s and g ought to be from empirical data it's pretty easy to tweak a production function to get steady state s and g to come out like you want.
Piketty does discuss Cobb-Douglas in the context of the capital/labor share of income (he not surprisingly thinks that the % going to capital will get bigger the higher k/y becomes).
There has been much discussion this week about Piketty’s use of net rather than gross savings. Using net savings allows him to derive a steady-rate k/y much higher than if he used gross savings (as most “conventional” models appears to do).
To my mind this seems to be pretty much a “sleight-of-hand” on his part – he adopts a model that drives the result he wants, without as far as I can see, ever justifying the use of that model.
Transformer, did you read Delong’s response to Krusall and Smith? Delong notes that Piketty discusses the exact equation that Krusall and Smith say that he is neglecting.
From note 12 on page 594:
“One can also write the law β = s / g with s standing for the total rather than the net rate of saving. In that case the law becomes β = s / (g + δ) (where δ now stands for the rate of depreciation of capital expressed as a percentage of the capital stock). For example, if the raw savings rate is s = 24%, and if the depreciation rate of the capital stock is δ = 2%, for a growth rate of g = 2%, then we obtain a capital income ratio β = s / (g + δ) = 600%. See the online technical appendix.”
I saw that,
In my view DeLong is bringing unnecessary heat into this discussion.
K&s are not saying Piketty is doing anything underhand. All they are are saying is “Piketty is using net savings and that leads to an increase in the k/s ratio compared to using gross savings . And also it leads to untenable results when g-0”.
DeLong doesn’t address that all – just talks abt the fact that K&S use 0.1 as the depreciation rate (which is a bit of a side-issue)
K actually responds here
http://ekonomistas.se/2014/05/29/krusell-och-smith-darfor-koper-vi-inte-pikettys-prognos/#comment-48153
What language is that, German?
In any case, Piketty seems to think that the equation that he uses, which is in terms of net savings, is actually equivalent to the formula that K&S give which uses gross savings.
Its Swedish I think.
And in Piketty’s example (from your extract) using gross savings and a depreciation rate of 2%, the k/s ratio halves from 1200% to 600% (which is the point K&S are making).
And even here he has chose a very low deprecation rate – 2%. If you chose a more realistic 3% or 4% then the difference between using gross and net saving becomes even more stark.
Thanks for responding, Dr. Murphy.
Here is a longer form of my argument, which is a bit more complicated than the obviously wrong strawman, “This chart from the BLS shows that productivity gains have translated into 0% growth in compensation for American workers since 1980.”
Economists can and do dispute whether productivity growth will necessarily lead to a rise in real compensation. Hanson and Cowen at GMU both do.
http://www.aei-ideas.org/2013/11/will-robots-terminate-the-us-middle-class-a-qa-with-tyler-cowen-author-of-average-is-over/
http://hanson.gmu.edu/aigrow.pdf
The chart proves nothing but that increases in productivity do not guarantee a uniform* level of compensation growth. The link between productivity and compensation is mediated through the ease of capital-labor substitution and differs between industries.
The claim that “they are going to be more physically productive per hour, and hence will be paid more” denies the possibility of cases in which productivity increases coexist with compensation decreases. The theoretical argument for this is weak and depends on there being a stage 4 economy beyond those of 1 (agriculture) 2 (industry), and 3 (finance/services) in which here is no large (<40% or so) segment of the population whose MPL < subsistence.
The key takeaway is that the ratio of gains from productivity captured by labor or capital is influenced by tech level, legal structure, unions, industry-specific factors, etc.
*I originally used the word "equal," which is imprecise and has many unfortunate connotations. "Uniform" gets the sense of my argument across better.
Let’s say that by law, all real hourly compensation had to be pegged precisely to productivity.
Beyond shutting down every union in the country, why would anyone ever voluntarily employ someone else?
Compensation tied to productivity just means people get to keep what they make.
However, on an assembly line it isn’t precisely clear how to achieve that, unless you had a bunch of meshing contracts between each party, and presumably people need to pay rent on any equipment that they use (unless they own that equipment themselves).
Compensation tied to productivity just means people get to keep what they make.
No, not exactly Tel; that’s the whole point of this post. “Productivity” here means output per man-hour. That’s not the same thing as “increment in output from an additional man-hour, all else equal.”
Hey everybody, two quick points:
(1) The Cobb-Douglas function has a *constant* share of output going to capital (and hence a possibly different constant share going to labor). So Piketty is actually using a Solow growth model, but not the special case of Cobb-Douglas. The function I’m using above isn’t Cobb-Douglas, because the output share goes to the factor that has more inputs. (Notice if labor grew more quickly than capital, then the wage rate would fall relative to the rental rate of capital, but that wage rate x units of labor would be higher than rental rate x units of capital.)
(2) The humongous problem with Piketty is that he says, “I don’t believe in Cobb-Douglas, I think capital share is increasing.” OK fair enough. But then he says (paraphrasing of course), “What I need is for elasticity of substitution to be above 1, and some empirical papers say that it is, so I think they best explain my historical work on capital concentration.” But the problem is, he’s misreading those empirical studies, because of the net/gross distinction. Since he is using a net model, but those empirical studies are using the more standard gross model, the fact that some of them have a parameter estimate in the range he thinks he needs, means nothing, because he’s comparing apples to oranges.
“But the problem is, he’s misreading those empirical studies, because of the net/gross distinction.”
Bob: can you point me to the section in the book where he does this ?
BTW: I’m not disputing what you saying – I’m just trying to understand).
transformer I can’t look it up right now, but maybe Summers cites it specifically?
I know that Summers says that elasticity of substitution is unlikely to be above 1 – I just wasn’t aware he had tied that to the net/gross savings thing.
I will take a look (more fun than doing my day job!)
You are correct: From Summers
“But I think he misreads the literature by conflating gross and net returns to capital. It is plausible that as the capital stock grows, the increment of output produced declines slowly, but there can be no question that depreciation increases proportionally. And it is the return net of depreciation that is relevant for capital accumulation. I know of no study suggesting that measuring output in net terms, the elasticity of substitution is greater than 1, and I know of quite a few suggesting the contrary. ”
All I need to do now is understand what that means 🙂
I guess he means that as the capital/output ratio increases the total % of income going to capital might in theory increase, but when you deduct the ever increasing amount that capitalists spend just replacing existing equipment then the net return as a % of total income is almost certain to fall (according to the studies that Summers is aware of ).
Yup, I totally missed the fact that Cobb-Douglas gives constant capital share when capital is paid it’s marginal product. My only defense is that I was trying to point out that an economy settling in to a constant s/g should be non controversial and I think a lot of different production functions will show that for you. And, won’t Cobb-Douglas work for Piketty’s argument as long as you are willing to by into the heavily (and correctly IMHO) disputed idea that the return on capital doesn’t change much?
And, won’t Cobb-Douglas work for Piketty’s argument as long as you are willing to by into the heavily (and correctly IMHO) disputed idea that the return on capital doesn’t change much?
I’m not sure which of “Piketty’s argument”s you mean, but no, if he’s trying to scare people into thinking the capitalists are going to squeeze out the workers, then he can’t use a Cobb-Douglas production function. If he did, then workers in 2100 would get paid the same fraction of total income that they get paid right now, even if capital stock compared to the size of GDP has quintupled.
Murphy, what you said about wages rising when productivity rises is true, but in the way you describe it, it is an argument that holds true for relative wages. When A becomes more productive than B, then A’s wage will tend to grow relative to B’s wage.
You are likely thinking in terms of absolute wage levels, and so in order to really counter the Marxists who believe, and/or want to convince people, that increases in labor productivity have a tendency in unfettered capitalism to “pass the workers by” and hoarded by capitalists, for that the marginal productivity theory of wages is insufficient. We have to move on and refer to the absolute productivity theory of wages instead.
Then add real world socialist money and banking when tends to raise capital income more so than labor income.