17
May
2014
Even More Inventory Scenarios
Tel and I have been going back and forth in the comments… He pointed out that if inventory grows at 2% forever (along with final sales), then GDP growth is a constant 2%. But be careful, what’s going on is that a constant 2% growth in inventories implies a constant 2% growth in the *change* in inventories, which is the relevant issue.
Below the first example shows what Tel is talking about, but the next two show what I am warning about. Note that inventory growth converges to 2% from both ends, even though GDP growth is a constant 2%.
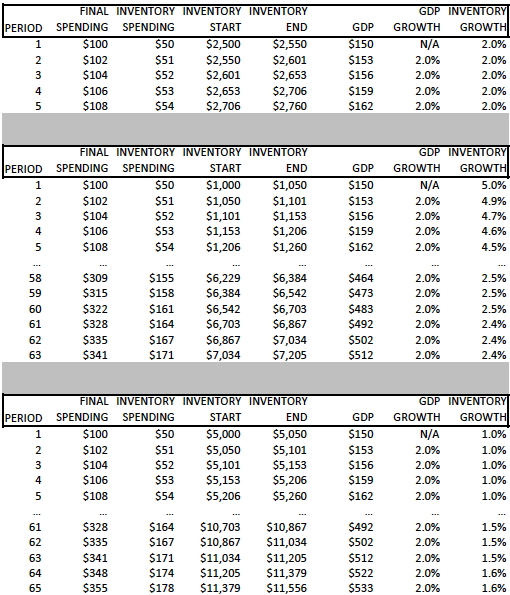







I guess my scenario is that if inventory growth is 2% and also sales growth is 2% then we know GDP growth is 2%.
You have demonstrated this does not work in reverse: if we see GDP growth is 2% and also sales growth is 2% then we can’t make an assumption about what inventory growth is going.
I just remembered that if all you know is the second derivative f”(t) but you don’t know the original function f(t) then you can use a double integration to find f(t) but the answer is not unique… knowledge of the initial conditions of the system would be required to find a unique answer.
On the second and third charts why is final spending 341 in period 63? Looks like it starts from 100 and goes up by 2 each period so it should be 224 by then (100 + (62*2)), right ?
I tried to reproduce your results and for me inventory growth converged on zero, not 2 and that may explain it.
oops, I see its increasing by 2% not 2. That’s it.
I think the biggest source of confusion is that the standard accounting identity for GDP includes consumption, which draws our attention away from production, which is what we’re actually trying to measure. In other words, GDP measures the *production* of final goods, and consumption is just the way to get there.
To arrive at production, we start with consumption and then add the amount of final goods that were produced but not consumed. This isn’t *wrong*. But it is confusing, as this whole episode shows.
One can imagine GDP accounting identities that don’t fall into this confusing trap. Ones that only look at production of final goods. Don’t look at consumption – that’s a distraction. Don’t look at inventory balances or their changes – that’s a distraction. Only look at production. The practical challenges of actually calculating GDP this way are probably to high to make this literally possible, but it’s helpful to at least think about.
Imagine if we treated the investment portion of GDP the way we treat consumption. In order to calculate investment, we would start with depreciation (or capital consumption), and then adjust depreciation by the change in capital stock. Again, this wouldn’t be *wrong*, but it’s obvious how this would cloud our thinking. We might start to worry about our machines not depreciating quickly enough, and become dismayed when higher production is caused by increases in our capital stock.
I think it was best said that GDP is the best bad tool we have.