Calling Sumner’s Bluff on Stock Prices and Inflation Expectations
Yesterday I put up a lengthy post arguing that Scott Sumner and Paul Krugman were inexplicably claiming vindication from data that, if anything, I would have thought they would prefer to sweep under the rug. Specifically, since 2008 the stock market’s movements have been much more strongly correlated with the spread between nominal and TIPS yields on 10-year Treasuries (which is a common benchmark of “the market’s expected rate of price inflation”). In Scott’s words, this shows the market has been “rooting for inflation” ever since the Fed fell asleep at the wheel in 2008 and let NGDP growth falter.
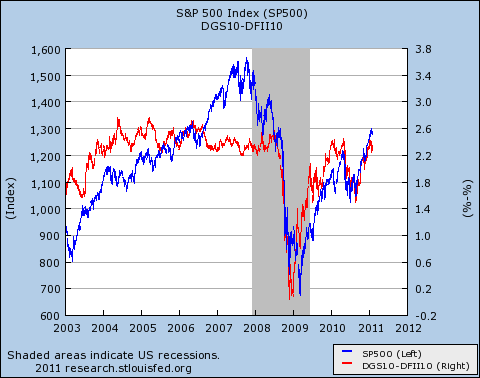
I pointed out that I would have thought just the opposite result would have vindicated Scott’s quasi-monetarist framework. In particular, if inflation expectations (as gauged by the spread between regular and TIPS yields) had stayed flat while the stock market zoomed upward in 2009 in response to QE1, then it would have been harder for people like me to say, “That surge in stock prices in artificial; it’s just another bubble.” (Granted, I would have said that, and with no embarrassment. I think Greenspan fueled a stock bubble with much more modest pumping than Big Ben.)
But as it turns out, I don’t have any splainin to do after all. The chart above (which Krugman actually created) has provided me with a nice little illustration showing that increases in the S&P 500 since the crisis began, have been almost perfectly matched with changes in inflation expectations.
In the comments of my post, Scott begged to differ. Here is a portion of his reply:
Bob, Only 4 problems with your post:
1. You misread the graph. It doesn’t show that stocks move in proportion to prices, the scale are vastly different. Stocks move much much more [than] prices, even prices changes cumulated over 10 years.
2. My model does not predict that all of extra NGDP growth will go into RGDP, that’s what Keynesians sometimes claim (the more extreme versions of Keynesians.) I ALWAYS assume an upward sloping SRAS, although I argue it is relatively [flat] in deep recessions. but never completely flat….
First let me paraphrase what Scott is saying here, to make sure the reader understands the back-and-forth between us titans: Scott is saying that in the chart above, just because the red and blue lines move hand-in-glove from 2008 onward, that does NOT mean we can attribute every change in stock prices to a recalculation by investors of inflation rates over the next 10 years. On the contrary, Scott claims that the stock market is moving more than the corresponding shifts in inflation expectations would warrant, but we’re not seeing that on the chart, because the axes have different scales.
But (here’s Scott’s point 2) it’s crucial to note that the direction is always the same, for both series, since 2008. This is (apparently) great news for Scott’s model, because his model says that if Bernanke gets investors to expect, say, 10% more NGDP in ten years, then (say) 8% of it will show up as increased RGDP in 2021, while the other 2% will push up the price level in 2021. (I’m using round numbers; you can’t really add up the percentages like that.)
So investors will push up current stock prices because of both factors–they expect stronger “real” earnings in 2021 (relative to their expectations before Bernanke convinced them he was a real man) and they expect higher prices in general in 2021. (Note that the absolute dollar-price of various stocks will be higher in 2021 on account of both factors, which is why investors bid up current prices for those same stocks.)
So does everyone get Scott’s point? Even though Bernanke’s promise of 10% more NGDP leads to 8% higher real output, it also pushes up prices (and hence current inflation expectations). Thus, when we’re in a situation (as Scott claims) where the big constraint on the economy is insufficient NGDP growth, you will see stock prices and inflation expectations moving in lockstep. In contrast, we didn’t see such a tight fit before the crisis, because there were lots of other factors that were important, and stalled NGDP wasn’t binding.
It’s a beautiful story. As I predicted (and note it was a falsifiable prediction, proving I am a man of science), Scott was able to explain how that chart was his ace in the hole, with all the i’s dotted and t’s crossed.
But as Columbo would say, I have just one more question: Should we take Scott’s word for it that the movement in stock prices is far greater than what could be attributed to a revision of inflation expectations? Since I had a bunch of pressing deadlines this morning at the office, I decided it was a perfect time to spend a half hour investigating Scott’s confident assertions.
First I checked the 10-year case. Just eyeballing the chart above, it looked like inflation expectations (over ten years) went from 0.2% to 2.4% from early 2009 to early 2011. During the same period, the S&P 500 went from 700 to 1300, an increase of 86%.
So the question is, could the jump in inflation expectations account for such a surge in stock prices?
The quick answer is “no.” If you had a stock worth $100 in 2009, and had it roll over at 0.2% for 10 years, it would be worth $$102.02 in 2019. In contrast, if that stock rolled over at 2.4%, it would be worth $126.77. So the change in expected average inflation rates could explain a 24% increase, but not an 86% one.
NOTE: Already this is awkward for Scott. Remember, he is saying that “the real problem is nominal.” So with unemployment above 9%, and people saying this is the worst slump since the Great Depression, it’s a bit weird to me that about 28% (=24%/86%) of The Ben Bernank’s stimulus gets soaked up by price inflation. In other words, that’s a pretty steep Short Run Aggregate Supply curve, eh?
NOTE #2: I also don’t think it’s right to say that investors just care about point estimates of inflation rates. For example, if The Bernank’s crazy policies since 2008 make investors think, “There is a 90% probability of 1% price inflation, a 9% probability of 4% inflation, and a 1% probability we go Zimbabwe,” you might see the stock and bond markets behave as the chart indicates. That is still more in the spirit of my worldview than Scott’s.
But back to the action: After seeing a victory (though admittedly slight) for Scott on a 10-year horizon, I thought, “Well why limit it to 10 years? After all, Scott thinks the market is so efficient that he literally doesn’t even believe in the possibility of bubbles. So what about doing the same analysis for 30-year bonds?”
Unfortunately, I don’t think FRED’s data on 30-year TIPS yields goes back far enough.
So then I tried 20-year bonds. And check this out:
First I figured out when the yields on 20-year Constant Maturity Treasuries bottomed out; it was 2.88% on December 30, 2008.
Then I looked up the 20-year TIPS yield on the same date: 2.20%.
Then I looked at the latest values (February 1, 2011 when I did the calculations) for both series: 4.37% for regular, and 1.81% for TIPS.
So the market’s 20-year average expected inflation rate (estimated using the method Scott and Krugman like) went from 0.68% to 2.56% during the period in question. Using the same approach of starting with a $100 stock and letting it roll over at the two rates for 20 years, you get an appreciation of 45% in equity prices that can be entirely attributed to the increased inflation expectations over 20 years.
Now the big question: How much did the actual S&P increase between December 30, 2008 and February 1, 2011? Well it went from 890.64 to 1307.59. That’s an increase of 47%.
So we see that Scott is still right on a 20-year time horizon: Changing inflation expectations can only account for 96% of the move in the S&P. That other 4% is property of the quasi-monetarists. Learn it, live it, love it.
Postscript
For what it’s worth, I really did accurately describe my approach above. In other words, I didn’t spend three hours searching through various bond series, and am now just reporting the one that worked. I checked the 10-year, saw it was promising, and then checked the 20, which I think Scott would have to agree is a better test of his worldview. Once I saw the result, I figured I could stop; my work was done here.
One other thing: I have checked the calculations, but hey I’m an Austrian economist and we’re not good with macro or math, so maybe I did something wrong, or maybe Scott will challenge the way I’m testing his assertion in the first place.
To be clear, I am not betting my worldview on the outcome of this calculation. Rather, I am pointing out that Scott’s claim of vindication doesn’t make any sense. It’s as if he took a Magic 8-Ball, asked it, “Does Bernanke need to print more money?” and then it said, “My sources say no.” Then Scott says, “A ha! I told you guys!”
In that context, I am merely saying, “Uh, if you’re gonna use that as your criterion, then you’re wrong. Not that I would have cared if it came out the other way.”







Loved the ending…
So we see that Scott is still right on a 20-year time horizon: Changing inflation expectations can only account for 96% of the move in the S&P. That other 4% is property of the quasi-monetarists. Learn it, live it, love it.
Money shot.
Bob, Why stop with 20 years? Use a consol (or perpetuity.) If the inflation expectation rises 1% on a perpertuity, the S&P 500 should go to infinity.
Of course this is reductio ad absurdum. I don’t understand your claim that stocks should rise by the amount of inflation expectations cumulated out to an arbitrary date in the future. Let’s say a company is worth $1 billion today, and is expected to be worth $1.1 billion in one year. Assume the nominal rate is 10%, so the $1.1 billion has a net present value of $1 billion, when discounted back to today. Now assume inflation expectations rise by 10%, so that the company is expected to be worth $1.21 billion in one year. Nominal rates will also rise by 10%, to 21% (including compounding) because of the Fisher effect. The NPV of the stock would still be $1 billion.
Now I’m certainly not claiming that things always work this smoothly, but you seem to be assuming no impact on the NPV formula at all. Unless I am missing something–this is my gut reaction after a quick read.
I had worried about this stuff too, Scott, and that’s why I acknowledged at the end that maybe you would challenge my approach.
But if I’m understanding your comment here, you are saying rational investors should always perfectly offset any expected inflation increase by insisting on higher nominal interest rates.
So when you said (in your comments on the last post) something to the effect that even if we allow a cumulative 10 years of extra inflation expectations, that can’t account for the jump in the S&P in recent years, what did you have in mind? I.e. how would you test your claim? Because to repeat, your comment right now suggests that it’s not even worth looking at the data; that we know a priori in an efficient market, changing inflation expectations can’t affect today’s nominal stock prices.
UPDATE on the above: I understand, Scott, that you are not saying efficient markets always perfectly offset it; you are just saying that would be the baseline case, and you want me to explain why I am completely ignoring that type of thing.
I agree with you. I admitted in the post itself, that you could very well challenge how I’m testing it.
But that’s why I’m now asking you, what did you mean in your comment to my original post? There it seemed you had some type of formula in mind, for assessing whether a given jump in stock prices and implied inflation expectations could be the whole story, and you said no it couldn’t.
So, what test were you using?
Yeah, the more I think about this, I think in the real world it would go something like this:
Let’s say Bernanke convinces everyone he is going to double the price level in 2020, compared to what we all thought yesterday that the price level would be in 2020.
So the immediate, disequilibrium reaction would presumably be that investors start dumping bonds and buying stocks (and land, gold, etc.).
Stock prices start going up while bond prices start falling. Eventually, equilibrium is restored when stock prices have risen enough so that–even accounting for the doubled nominal stock prices in 2020–the implied nominal rate of return on stocks over the next 9 years is comparable to the new, much higher rate of return you could earn on bonds. (Of course you adjust for the riskiness of stocks vs. bonds.)
So in my main post above, I was implicitly assuming that the stock prices would do all the work; i.e. they’d shoot up so much now, that the rate of return on holding stocks would be no higher than the (same) rate of return on holding bonds.
On the other hand, in your comment you were implicitly assuming that the bond prices would do all the work; i.e. they’d drop down so much, that their rate of return would match the incredible rate of return from holding stocks which were worth the same amount now as before.
In the real world, I would guess it would be be somewhere in between those two extremes, but I’m having a mental block in figuring out what else would pin it down. Presumably there would be some other things through which arbitrage would make it tend toward one or the other ends of the spectrum.
Duh OK one obvious thing that would also happen, is that the demand to hold money balances would plummet. So that would cause the price level in 2011 to start rising too, which would take the pressure off falling bond prices. I.e. the discount on 2021 dollars wouldn’t need to be as severe, as 2011 dollars became weaker and weaker.
Heh so now I think we’re back to my original scenario, right? Suppose we live in a Chicago School world where all prices are perfectly flexible and everybody is as rational as Scott Sumner. People learn that Bernanke is going to make prices in 2021 double what they originally thought (yesterday).
So all prices in 2011 immediately double, including stock prices. There is no reason for nominal interest rates to change, because the expected change in the purchasing power of the dollar between 2011 and 2020 is back to what it was, yesterday.
* * *
Obviously this isn’t what happens in the real world; our old friend sticky prices screw everything up as usual. In the real world, prices in 2011 won’t instantly double. So that means nominal interest rates will in fact rise (i.e. bond prices fall), which (ceteris paribus) would arrest the increase in stock prices, and keep them from doubling instantly.
It would really make our jobs easier if prices were perfectly flexible.
Bob, I should warn you that the model I had in mind may be wrong. I’ve always suppected that the Fisher effect worked mostly for flexible prices, not sticky prices. If some prices are sticky, then a 10% monetary shock might cause sticky porices to rise 2% a year for 5 years, but flexible prices might immediately rise by 10%. I’ve also assumed that in that case, there may be no Fisher effect, as the sorts of goods that are good alternatives to financial assets (commodities, real estate, etc) tend to be the more flexible price goods. If ther erise immediately, ther eis no further expected rise over 5 years. If there is no Fisher effect, stocks might immediately rise by 10%, as you say. Here’s what limits your argument above. This only works for as long as regular goods prices are stcky. You can plausibly push that out a few years, but not 20, 30, 40 etc.
Again, this is my own take on things, others might see it differently. But you definitely can’t just pick a super long term bond, and start cumulating price increases, because over the very long term there is some Fisher effect will will impact the NPV formula.
I agree that my previous response was slighly misleading, as I didn’t spell out my assumptions.
Fair enough. In my defense, I think I was doing exactly what your retort suggested, but in retrospect I agree that you were sort of sticking your neck out just to prove how confident you were.
I.e. you were saying, “Bob, even if you looked at the cumulative rise in prices over ten years, that can’t explain the jump in the S&P. So clearly this isn’t just about inflation expectations.”
So that statement doesn’t mean that the proper way to actually estimate the effect of inflation expectations, is to look at the cumulative change at the end of some horizon.
Here’s what limits your argument above. This only works for as long as regular goods prices are stcky. You can plausibly push that out a few years, but not 20, 30, 40 etc.
Not sure I get that. If prices aren’t sticky, then they should rise in response to the expected future inflation (bringing it into the present).
I.e. the way I’m thinking about it, it’s sticky prices that keep alive the Fisher effect you are talking about. The only reason bond prices fall, is that the purchasing power of money doesn’t immediately fall to reflect the new expectations. So that’s why the exchange rate between present and future dollars has to change. Then, this increase in nominal interest rates is what limits the appreciation of current stock prices.
Confused.
If, in an EMH world, stock prices are determined by long term expectations of real growth, then why would stock prices show the close correlation in the above chart? The presence of any sticky prices will presumably be factored into 10 year estimates of inflation and reduce the correlation (by increasing temporary real price effects and reducing average expected observed inflation). Uncertainty over the path of future monetary policy would presumably increase stickiness (given menu costs).
Doesn’t the stock price impact depend too on whether the monetary policy is perceived to be one-time or ongoing?
On the other hand, perhaps both stock prices and inflation expectations are/can be direct indicators of monetary disequilibrium (amongst other things, in the case of stock prices) and that’s why they are moving together which, I would have thought was consistent with both the Bob Murphy story and the Scott Sumner story.
In fact, I had the (perhaps mistaken) impression that it was tacitly recognized by some supporters of QE2 that the resulting increase in stock prices would be driven by more than simply improved expectations of real growth.