Free Advice

In case people are confused, Paul Krugman drives me bananas not because he’s a Keynesian, but because he’s an unfair bully who mocks people on his blog. Look at this:

2. Paul Ryan requires that his staffers read Atlas Shrugged. I mean, I was inspired by Isaac Asimov, but I don’t think I’m Hari Seldon — whereas Ryan, it seems, really does think he’s John Galt.Time to bring out the classic quote:

There are two novels that can change a bookish fourteen-year old’s life: The Lord of the Rings and Atlas Shrugged. One is a childish fantasy that often engenders a lifelong obsession with its unbelievable heroes, leading to an emotionally stunted, socially crippled adulthood, unable to deal with the real world. The other, of course, involves orcs.

Future historians will giggle at our expense.

Now it’s good that Krugman engaged in a pre-emptive strike on himself; he couldn’t merely mock Ryan for being a fan of a novel, because in the New Yorker profile of Krugman we read:

Krugman explained that he’d become an economist because of science fiction. When he was a boy, he’d read Isaac Asimov’s “Foundation” trilogy and become obsessed with the central character, Hari Seldon. Seldon was a “psychohistorian”—a scientist with such a precise understanding of the mechanics of society that he could predict the course of events thousands of years into the future and save mankind from centuries of barbarism. He couldn’t predict individual behavior—that was too hard—but it didn’t matter, because history was determined not by individuals but by laws and hidden forces. “If you read other genres of fiction, you can learn about the way people are and the way society is,” Krugman said to the audience, “but you don’t get very much thinking about why are things the way they are, or what might make them different. What would happen if ?”

With Hari Seldon in mind, Krugman went to Yale, in 1970, intending to study history, but he felt that history was too much about what and not enough about why, so he ended up in economics. Economics, he found, examined the same infinitely complicated social reality that history did but, instead of elucidating its complexity, looked for patterns and rules that made the complexity seem simple. Why did some societies have serfs or slaves and others not? You could talk about culture and national character and climate and changing mores and heroes and revolts and the history of agriculture and the Romans and the Christians and the Middle Ages and all the rest of it; or, like Krugman’s economics teacher Evsey Domar, you could argue that if peasants are barely surviving there’s no point in enslaving them, because they have nothing to give you, but if good new land becomes available it makes sense to enslave them, because you can skim off the difference between their output and what it takes to keep them alive. Suddenly, a simple story made sense of a huge and baffling swath of reality, and Krugman found that enormously satisfying.

OK, so since Krugman says he’s not nearly as weird as Paul Ryan, surely if we follow Krugman’s link, we’ll read that Paul Ryan…I don’t know, is building a gulch somewhere. Nope, here it is:

Representative Paul Ryan, also of Wisconsin, requires staffers to read Atlas Shrugged, describes Obama’s economic policies as “something right out of an Ayn Rand novel,” and calls Rand “the reason I got involved in public service.”

and

“The reason I got involved in public service, by and large, if I had to credit one thinker, one person, it would be Ayn Rand,” Ryan said at a D.C. gathering four years ago honoring the author of “Atlas Shrugged” and “The Fountainhead.” …

At the Rand celebration he spoke at in 2005, Ryan invoked the central theme of Rand’s writings when he told his audience that, “Almost every fight we are involved in here on Capitol Hill … is a fight that usually comes down to one conflict–individualism versus collectivism.”

So you can see why Paul Ryan is a geeky weirdo who lives in fantasy land, whereas Krugman was probably the homecoming king in high school such is his cool machismo.

(Just to be clear, I don’t think I am the Italian Stallion. In fact, Italians and Irish often don’t get along.)

30 Dec 2010

Krugman In Support of the Hangover Theory?

Economics, Krugman 9 Comments

I know, I know, I should stop trying to spot Krugman Kontradictions; the antinomies in his writing merely reflect my mortal mind’s attempt to absorb the infinite.

Lately Krugman has been patting himself on the back for his skepticism about the viability of the euro. He finds it hilarious that two economists published a “duh, what idiots” article on these skeptics, basically just before the euro crisis set in. (I too found that funny; I’ll give Krugman that one.)

Now relying on the theory of “optimal currency areas,” Krugman says that we should have expected the euro-zone to be more vulnerable to crises than the United States:

What was behind those doubts? People like me and Barry Eichengreen — who did more than anyone else to turn the abstract arguments into quantitative research — thought of the euro in terms of the theory of the “optimum currency area”. This theory says that there are both benefits and costs to adopting a common currency. The benefit is reduced costs of doing business; the cost is that it’s harder to get your costs and prices back in line after “asymmetric shocks” — booms and slumps that affect some countries in a currency union but not others.

Both the benefits and the costs are hard to quantify, but there are some indicators you can look at. If the benefits of a common currency are large, you’d expect forming that currency to lead to a large increase in trade. Meanwhile, the costs of difficult adjustment depend on how much adjustment you need to make. The burden is reduced if labor is highly mobile between booming and slumping regions (Mundell’s point) and if you have fiscal integration (a point made by my colleague Peter Kenen)…

OK, now that you have the general idea, check out Krugman’s post yesterday where he compares Nevada and Ireland:

As part of a project I’ve been working on, I’ve been doing some US-Europe comparisons, and have a curious parallel: by the numbers, Ireland looks a lot like Nevada. The populations are similar; the housing bubbles were comparable in their extremity; both currently have roughly 14 percent unemployment.

The comparison also highlights some of the reasons Europe is having more trouble with a single currency than the United States. In both places, emigration is a safety valve — but even though the Irish are unusually mobile by European standards, they probably won’t leave as readily as the workers who moved to Nevada in the boom years.

To be sure, Krugman goes on to talk about other factors. But if I didn’t know any better, just reading the above, I would think that the boom period was characterized by workers flowing into Nevada, and the recovery will be speedier to the extent that those workers get the heck out of dodge and go somewhere else in the economy.

Doesn’t this sound a lot like the hangover theory that Krugman ridiculed? (Specifically, Krugman set up his target by quoting John Cochrane: “We should have a recession,” Cochrane said in November, speaking to students and investors in a conference room that looks out on Lake Michigan. “People who spend their lives pounding nails in Nevada need something else to do.”)

Couldn’t Arnold Kling have written the above, in support of his Recalculation argument?

I know, I know, there is no contradiction here. Cochrane is a moron for thinking the way to end the recession is for workers to leave Nevada, whereas Krugman is a genius for predicting that Europe’s recessions would be worse since their workers can’t move around as easily as Nevadans. Krugman Kannot Kontradict.

30 Dec 2010

Is Big Government a Myth?

Economics, Shameless Self-Promotion 9 Comments

My sources say no:

Lately the supporters of big government have deployed an interesting twist to their arguments, claiming that it is a dirty right-wing lie that government has grown under the Obama administration. Unlike arguments over economic theory, surely this should be an objective exercise in looking up the facts.

As we’ll see, yes Virginia there is indeed a big — and growing — government in DC, as even that government’s own numbers confirm. Although this conclusion won’t surprise the readers of this column, it will still be fun to analyze Paul Krugman’s attempts to deny the obvious.

Now I know you Krugman lovers will be able to explain everything away; don’t disappointment me.

29 Dec 2010

Fallacies Multiplying Like Rabbits

All Posts 20 Comments

[Non-typo UPDATE below.]

OK I need to get this out of my system, so I can proceed to more important things… If you need to get up to speed on Landsburg’s population brain teaser, go to this post. Here, I am going to assume every reader is hip deep in the problem and needs my careful coaching to escape the black hole into which I nearly fell myself, lo this past fortnight.

So here are my thoughts:

* I am assuming we are talking about the population of children (not the parents), and that nobody dies. The kids don’t in turn reproduce; there is just an initial set of couples, who then start cranking out babies.

* I am not dead certain, but I am very very confident, that Landsburg’s (modest) point is correct. In particular, I think if we did computer simulations, he would win. That is to say, for any finite number C of couples, and for any finite number G of generations (where in principle, a given couple could have a string of G girls and not a boy when the cutoff is reached), if we ran that simulation a large but finite number S times, we would observe: (A) More often than not, the population would have more boys than girls, and (B) for each of the S simulations, if we calculated the fraction of girls in the population (of children), and then took the mean of that calculation over all S simulations, the answer would be lower than 0.5.

* The important thing going on here is that “mathematical expectation” means something very specific, and in some contexts it is misleading. For example, consider two independent, random variables X and Y that are each uniformly distributed on the interview [1, 2]. The expectation of each is the midpoint, i.e. 1.5. However, if you calculate the expectation of (X/Y) it is bigger than 1. (Specifically it’s 3ln(2)/2.) Of course by symmetry that means the expectation of (Y/X) > 1 as well. So at first glance that’s weird. It seems like you’re saying you “expect” X to be bigger than Y, and Y to be bigger than X, at the same time. But that’s not what you’re saying. The general moral is that the ratio of expectations is not equal to the expectation of the ratio. I.e. even though E(X) = E(Y), it’s not true that E(X/Y) = 1, even though these are independent variables.

* Back to the population puzzler: Yes, it is certainly true that nature doesn’t care what rules the couples are using. Every time someone has another kid, there is a 50/50 chance it is a girl. But this doesn’t prove what a lot of people think it does. It’s true that within any population, or even within an individual family, the expected number of boys equals the expected number of girls. I.e. E(G) = E(B). But as we just saw, that fact by itself doesn’t mean we can conclude that E(G/B) = 1, or that E(G/(G+B)) = 0.5

* What IS true is that if we look at the entire set of children IN ALL POSSIBLE POPULATIONS, then E(G/(G+B)) = 0.5. But that’s not what the question asked.

* What Landsburg interpreted the question as asking, is the mathematical expectation of the fraction of girls *for any particular population* that is randomly drawn from the set of all possible populations. For populations consisting of any finite C number of initial couples (who then crank out kids), that answer is quite simply NOT 0.5. It’s true, as C goes to infinity, the answer approaches infinity. It’s also true that most people would have assumed that the spirit of the question meant, “For arbitrarily large populations.” But Landsburg (quite fairly, in my opinion) doesn’t think this means the basic intuition is right. No, people are skipping a huge step in the problem, when they go from the observation “each child is 50/50 a girl” to “I think in a large enough population, the expected fraction of girls is 50%.”

* Specifically, here’s what’s going on: The set of all possible populations has populations with DIFFERENT SIZES. There are a bunch of possible populations where many of the couples have one boy and no girls. In such populations, the fraction of girls is less than 0.5. On the other hand, there are a bunch of possible populations where many of the couples have tons of girls, and one boy. In such populations, the fraction of girls is greater than 0.5. However, if we assign the same weight to each potential population, even though some have more children than others, then the mean of all such fractions will be smaller than 0.5. In other words, in fewer than 50% of the possible populations, will there be more girls than boys.

* We know this is correct, and ironically, for the very reason that the Landsburg-haters keep harping on. Clearly, in the whole UNIVERSE of possible populations, the ratio is 0.5. In other words, there are as many boys as girls, if we look at the entire group of “possible children” in the universe. Now then, in one potential population that has more boys than girls, how is that going to happen? With the particular stopping rule under consideration, that will only happen when there are a lot of families with just one boy, and not so many families with a ton of girls. In contrast, the potential populations with more girls, will be ones where there aren’t many families with just one boy, i.e. there are a lot of families who had a string of girls before getting a boy. So this means that for a finite C number of couples, if you look at populations with more boys than girls, you will see small populations, while if you look at populations with more girls than boys, you will see big populations.

* Do the Landsburg Haters feel the vice closing? If you already admit–proudly in fact–that in the total universe of all possible offspring, there is an equal number of boys and girls, and you now see (though perhaps you didn’t think about it much before) that an actual population with more boys will have a smaller population, while a population with more girls will have a big population, then maybe it is dawning on you what Landsburg is saying: There are MORE POPULATIONS with a ratio of girls smaller than 0.5. The way the “total offspring in all possible populations” achieves the perfect 0.5 ratio, is that there are a (relatively small) number of possible populations with a ton of girls. You can’t have it both ways: If you still insist that in any randomly drawn population, the ratio of girls is just as likely to be under as over 0.5, then you must think that in the set of all possible offspring (across all potential populations), there are more girls than boys. (Or, you must deny that populations with a higher ratio of girls, have more total children than populations with a smaller ratio of girls.)

* This might help it click for some of you: Suppose we assume there are 1 billion couples, and we cut a simulated computer run off after 1000 generations. There is one potential outcome in which there are 1 billion boys, and 0 girls. The ratio of girls to boys in this outcome is 0. There is also a potential outcome in which there are 0 boys and 1 trillion girls. (Each of the billion couples has a string of 1000 girls without getting a boy, and then the simulation ends.) The ratio of girls to boys in this outcome is 1. But it is far more likely than an actual simulation will hit that first outcome than the second, so the 0% value of girls will get a much higher weight (to calculate the expectation) than the 100% value will get. Note that it’s still true that for any given simulation, the expected number of girls equals the expected number of boys (I think it’s 1 billion girls and 1 billion boys?). What’s happening is that there is a small probability of getting a bunch of girls, and that drives up the expectation of the number of girls. But no matter how many girls there are, the fraction can’t ever be higher than 100%. So that’s the most such an outcome can “push up” the overall expectation of the *fraction*.

* So for all these reasons, I think Landsburg is basically correct, and that simulations would show this. However, let me now give a shout out to his critics…

* Most important, I think Landsburg has seized on a particular formulation of the problem that misses the spirit of the puzzle. I think the point of the question is, “Should we expect this type of parental stopping rule to give a tendency for more boys?” At first you think, “Of course it would!” but then you realize, “Wait a second, there are no men with brothers in this society, but some guys have a ton of sisters…” So you try to use intuition to figure out if the families with 1 boy more than offset the families with a ton of girls, and you then have the “aha!” moment and realize that we have no reason to expect there to be more boys than girls. In other words, if someone in a job interview described the couples’ intentions and then said, “So, if we let this population grow for many centuries and then took a look, would you expect to see more males or females?” I think that would be fine. That is the interesting part of the puzzle, not the quirks of the Expectation operator.

* The physicist makes a good point that the standard approach for calculating probabilities takes a family (or group of families) and runs through the various scenarios of how they could come up with a boy. In other words, the probability of a given family having 0 boys is 0, the way everybody is tackling this problem. And yet, if we want our answer to reflect a humongous (but finite) population in progress, surely it is stacking the deck in favor of the boys to do it this way.

* Extending the last point, what if we captured the finite aspect of it, not by taking C couples, but rather by fixing O total offspring? In other words, what if we said, “Choose any finite O number of total offspring for the population. What is the expectation of the fraction of girls?” I’m pretty sure the answer is 50%. The reason nobody models it this way, is that it’s not nearly as intuitive as taking the couple approach, because it gets tricky to figure out all the ways you could generate that many offspring. For example, for O = 1, you clearly are dealing with only one couple, and the answer is obviously 50%. For O = 2, you could be dealing with 1 or 2 couples. (If 1 couple, then 2 generations, while if 2 couples, then 1 generation.) I haven’t done this rigorously, but I’m pretty sure if you do it this way, for any finite O, the expected fraction of girls is 0.5. UPDATE: Actually this approach is much weirder than the couple approach, because you can’t come up with a good way of assigning probabilities to the different scenarios. E.g. with O = 2, if there’s 1 couple then the proportion of girls is 100% half the time, and 50% the other half. So the expected proportion of girls is 75%. But if there are 2 couples then it’s one generation and a coin toss, so the expected proportion of girls is 50%. But to figure out the overall expected proportion of girls, conditional on O = 2, you need to know how likely it is that there is 1 couple versus 2 couples. But that doesn’t really make any sense. (Also, for this particular O, notice that regardless of the probabilities, the expected proportion of girls is higher than 50%, unless I did something stupid. So probably the intuition of “let’s focus on the offspring, not the couples” is not nearly as good as I thought ten minutes ago.)

* As I said, there is no reason that the finite O approach is any stranger than the finite C approach, except for the fact that when we picture a specific iteration of the random process, we are picturing an initial group of couples who then throw on Barry White. But I think Landsburg is not giving due credit to his critics who are really upset at his particular approach to the solution, when alternate (and equally plausible) approaches would vindicate the “wrong” intuition.

* This leads to my final point: It is absolutely hilarious to see how heated the debate got in the comments at Landsburg’s blog. Landsburg kept calling one guy “too stupid to understand this,” and–surprise!–that only made the guy angrier. If people can have this much controversy and bullheadedness over a problem that is 95% math, no wonder we can’t get anywhere in the social sciences.

29 Dec 2010

And the Winner of the Most Implausible Blog Statement of 2010 Is…

Federal Reserve No Comments

…Scott Sumner!

Just to clarify, “Implausible Blog Statement” means “statement someone made on a blog, that is not likely to be true.” After all, it would be very implausible that someone would post on a blog, “I just took a bath with my toaster.” But that’s not what I mean with this category.

After praising Don Luskin’s thoroughly obnoxious appearance on the Kudlow show, Scott Sumner proceeded to school me in the comments of his post with this answer to my question:

Bob, The Fed’s policies of the last three years have made things really hard for the federal government, as the Fed has caused inflation to fall to the lowest level in my lifetime, which is bad news for the world’s biggest borrower (Uncle Sam.) That’s why the US fiscal position is getting much worse–because of the Fed.

That strikes me as absurd. For one thing, everybody knows that it’s not price inflation, but NGDP growth, that debtors care about. (A little joke there for ya.)

But more seriously, the federal government has added a ton of debt in the last three years, and it plans on adding a lot more in the next few years. So it’s not like we’re looking at a guy who bought a house three years ago and then (price) inflation expectations collapsed.

Furthermore, because of the Fed (I claim) nominal interest rates on newly issued Treasury debt have been much lower than they otherwise would have been.

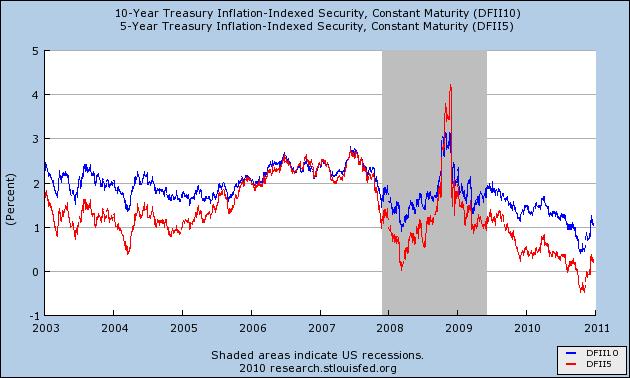
I think Scott is a big fan of TIPS yields. Roughly speaking, that should take into account the nominal/price inflation effects, and show the real cost of government borrowing. And except for that spike (which is Scott’s smoking gun for his thesis that Bernanke was too tight in the fall of 2008), it sure looks to me like the government has been able to borrow more cheaply during the crisis than was the norm before:

29 Dec 2010

Surreal

Economics, Humor 7 Comments

I was picking my son up from the airport. Since he is a little guy, I had to get a pass and go through security, so that I could meet him at the gate as soon as he got off the plane.

Because of the Northeast fiasco, I got to the airport really early in case there were long lines. I brought Mises’ Theory of Money and Credit to pass the time–always a fun book when you have a spare hour.

As I’m approach the security line, a TSA guy–a white guy in his late 40s or early 50s I’d say–asks me what book I’m reading. I show it to him and explain, “I’m an economist and I have to review it.” (I’m actually writing a study guide, but no need to give the government more help in thwarting the Institute’s mission of free-market education.)

I was stunned when the guy answered, “Oh good stuff. Have you ever read Bastiat?”

I said of course. Then he said, “Yeah Bastiat…though he’d be rolling over in his grave now.”

Then the guy started talking about an investment book he was reading. I actually had to let people cut me in line because he wasn’t done discussing.

28 Dec 2010

What Fraction of His Money Do You Expect Landsburg to Lose?

All Posts 23 Comments

I am ashamed to admit how many hours in the last few days I have devoted to this silly problem I first read on Steve Landsburg’s blog:

There’s a certain country where everybody wants to have a son. Therefore each couple keeps having children until they have a boy; then they stop. What fraction of the population is female?

Well, of course, you can’t know for sure, because, by some extraordinary coincidence, the last 100,000 families in a row might have gotten boys on the first try. But in expectation, what fraction of the population is female? In other words, if there were many such countries, what fraction would you expect to observe on average?

I have many things to say about it–my brother (who was in a PhD math program) and I argued for a good hour last night alone. But I am way behind on “real work” and so can’t do it justice.

This is not for everyone, but for those who are geeky enough, it’s actually pretty interesting to delve into this controversy. So here’s my plan for you, to get up to speed such that you will fully appreciate my attempt to resolve the dispute when I post it at some unspecified time in the future:

(1) Read Landsburg’s original statement of the problem. Try to figure it out yourself, then skim the comments to see all the knots his readers tied themselves into.

(2) Read Landsburg’s purported solution.

(3) Read the physicist who thinks Landsburg is wrong.

(4) Go back to the comments of Landsburg’s solution post, and skim them. A few people keep hitting on the key elements of the controversy. (To give you a hint: It’s crucial that not every “potential population” has the same size.)

(5) Finally go read Landsburg’s $15,000 challenge to the physicist.